高中数学 16 三角函数模型的简单应用2课件 新人教A版必修4 课件VIP免费

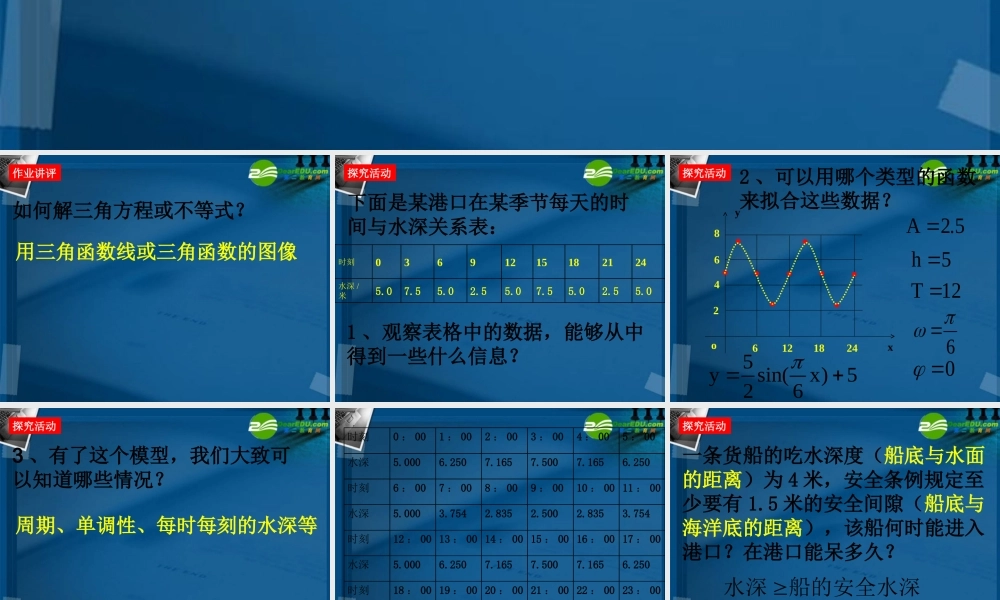
1.6 三角函数模型的简单应用 第二课时 高一数学必修 4 第一章 如何解三角方程或不等式？用三角函数线或三角函数的图像 作业讲评1 、观察表格中的数据，能够从中得到一些什么信息？ 5.02.55.07.55.02.55.07.55.0水深 /米24211815129630时刻下面是某港口在某季节每天的时间与水深关系表：探究活动2 、可以用哪个类型的函数来拟合这些数据？yo18246122468x探究活动h56 A2.5T125ysin(x)5260 3 、有了这个模型，我们大致可以知道哪些情况？ 周期、单调性、每时每刻的水深等 探究活动3.7542.8352.5002.8353.7545.000水深23 ： 0022 ： 0021 ： 0020 ： 0019 ： 0018 ： 00时刻6.2507.1657.5007.1656.2505.000水深17 ： 0016 ： 0015 ： 0014 ： 0013 ： 0012 ： 00时刻3.7542.8352.5002.8353.7545.000水深11 ： 0010 ： 009 ： 008 ： 007 ： 006 ： 00时刻6.2507.1657.5007.1656.2505.000水深5 ： 004 ： 003 ： 002 ： 001 ： 000 ： 00时刻一条货船的吃水深度（船底与水面的距离）为 4 米，安全条例规定至少要有 1.5 米的安全间隙（船底与海洋底的距离），该船何时能进入港口？在港口能呆多久？5.1456sin5.2x探究活动水深船的安全水深yo18246122468x探究活动5ysin(x)526yo18246122468x5ysin(x)5265.1456sin5.2x2.06sinx即y=5.5ABCD0.3846,5.6154xxAB12.3846,17.6154xxCD 货船可以在 0 时 30 分左右进港，早晨 5 时 30 分左右出港；或在中午 12 时30 分左右进港，下午 17 时 30 分左右出港 . 每次可以在港口停留 5 小时左右 .探究活动若某船的吃水深度为 4 米，安全间隙为 1.5 米，该船在 2 ： 00 开始卸货，吃水深度以每小时 0.3 米的速度减少，那么该船在什么时间必须停止卸货，将船驶向较深的水域？探究活动2.5sin55.50.3(2)(2)6xxx典例分析P船停止卸货时，必须水的深度≥船的安全水深26x8 10 12y4y=-0.3x+6.1o24682.5sin56yxp=+ 时间实际水深 安全水深 是否安全典例分析6 ． 54 ． 2 米 4 ． 1 米 较安全7 ． 03 ． 8 米4 ． 0 米危险6 ． 05 米4 ． 3 米安全P 点的坐标如何求得呢？数形结合，二分法求近似解：货船最好在 6.5 时之前停止卸货，将船驶向较深的水域 . 26x8 10 12y4y=-0.3x+6.1o24682.5sin56yxp=+P.1. 根据...