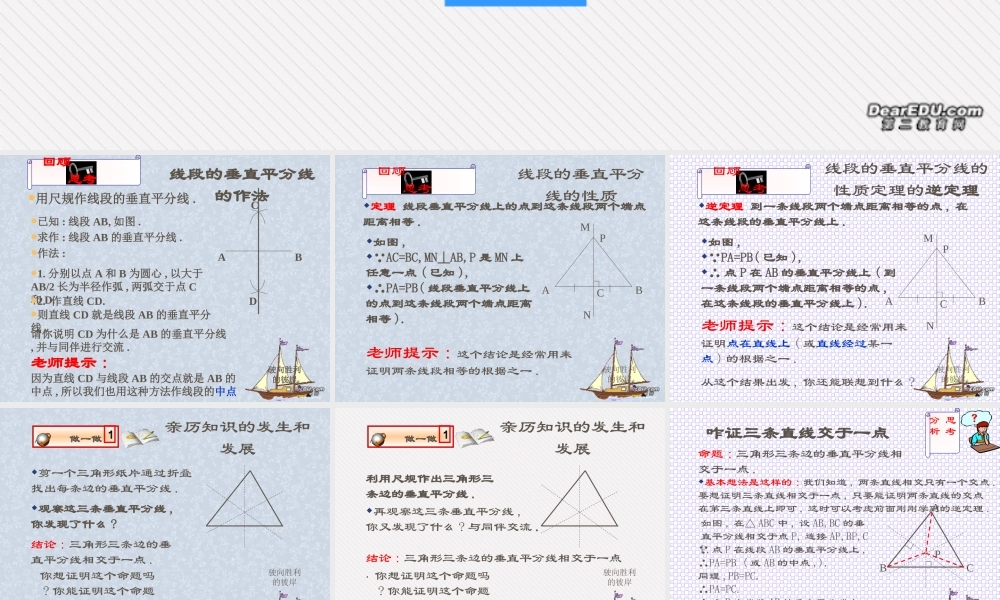
3. 线段的垂直平分线( 2 ) 三角形的垂心驶向胜利的彼岸线段的垂直平分线的作法已知 : 线段 AB, 如图 .求作 : 线段 AB 的垂直平分线 .作法 :用尺规作线段的垂直平分线 .1. 分别以点 A 和 B 为圆心 , 以大于AB/2 长为半径作弧 , 两弧交于点 C和 D.ABCD2. 作直线 CD.则直线 CD 就是线段 AB 的垂直平分线 .请你说明 CD 为什么是 AB 的垂直平分线, 并与同伴进行交流 .老师提示 :因为直线 CD 与线段 AB 的交点就是 AB 的中点 , 所以我们也用这种方法作线段的中点.回顾 思考驶向胜利的彼岸线段的垂直平分线的性质定理 线段垂直平分线上的点到这条线段两个端点距离相等 .老师提示 : 这个结论是经常用来证明两条线段相等的根据之一 .ACBPMN如图 , AC=BC,MN⊥AB,P 是 MN 上任意一点 ( 已知 ),∴PA=PB( 线段垂直平分线上的点到这条线段两个端点距离相等 ).回顾 思考驶向胜利的彼岸线段的垂直平分线的性质定理的逆定理逆定理 到一条线段两个端点距离相等的点 , 在这条线段的垂直平分线上 .ACBPMN如图 , PA=PB( 已知 ),∴ 点 P 在 AB 的垂直平分线上 ( 到一条线段两个端点距离相等的点 ,在这条线段的垂直平分线上 ).老师提示 : 这个结论是经常用来证明点在直线上 ( 或直线经过某一点 ) 的根据之一 .从这个结果出发 , 你还能联想到什么 ?回顾 思考驶向胜利的彼岸亲历知识的发生和发展剪一个三角形纸片通过折叠找出每条边的垂直平分线 .结论 : 三角形三条边的垂直平分线相交于一点 .老师期望 :你能写出规范的证明过程 .你想证明这个命题吗? 你能证明这个命题吗 ?观察这三条垂直平分线 ,你发现了什么 ? 做一做 11驶向胜利的彼岸亲历知识的发生和发展利用尺规作出三角形三条边的垂直平分线 .结论 : 三角形三条边的垂直平分线相交于一点.老师期望 :你能写出规范的证明过程 .你想证明这个命题吗? 你能证明这个命题吗 ? 做一做 11再观察这三条垂直平分线 ,你又发现了什么 ? 与同伴交流 .驶向胜利的彼岸思考分析命题 : 三角形三条边的垂直平分线相交于一点 .如图 , 在△ ABC 中 , 设 AB,BC 的垂直平分线相交于点 P, 连接 AP,BP,CP. 点 P 在线段 AB 的垂直平分线上 ,∴PA=PB ( 或 AB 的中点 ,).同理 ,PB=PC.∴PA=PC.∴ 点 P 在线段 AB 的垂直平分线上 ,∴AB,BC,AC ...