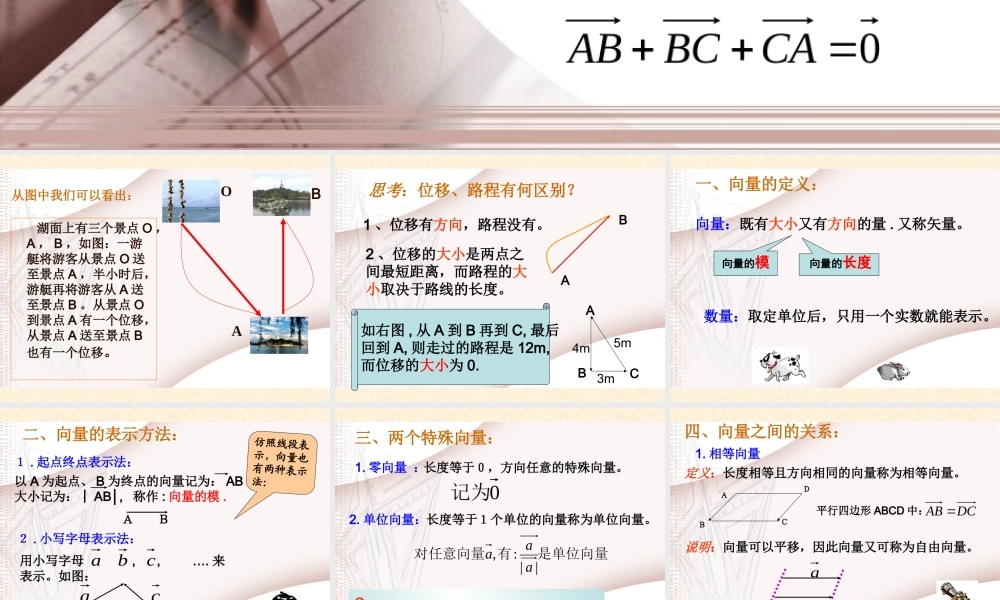
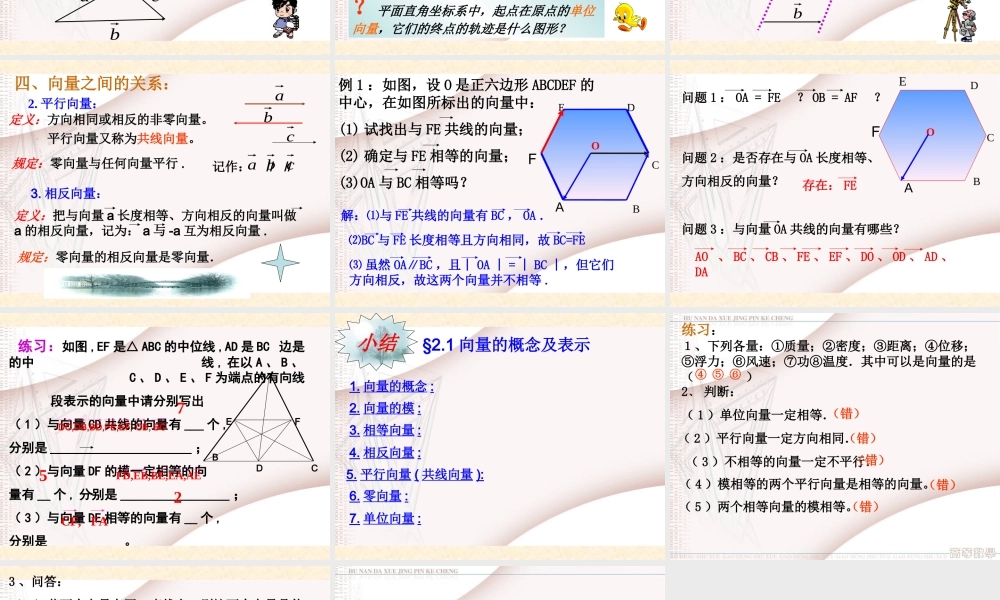
§2.1 向量的概念及表示0CABCABBAAB 湖面上有三个景点 O ,A , B ,如图:一游艇将游客从景点 O 送至景点 A ,半小时后,游艇再将游客从 A 送至景点 B 。从景点 O到景点 A 有一个位移,从景点 A 送至景点 B也有一个位移。OBA从图中我们可以看出: 思考:位移、路程有何区别?1 、位移有方向,路程没有。2 、位移的大小是两点之间最短距离,而路程的大小取决于路线的长度。ABABC4m3m5m如右图 , 从 A 到 B 再到 C, 最后回到 A, 则走过的路程是 12m,而位移的大小为 0. 数量:取定单位后,只用一个实数就能表示。向量:既有大小又有方向的量 . 又称矢量。向量的模向量的长度一、向量的定义: 二、向量的表示方法:仿照线段表示,向量也有两种表示法:1 . 起点终点表示法:以 A 为起点、 B 为终点的向量记为: AB大小记为:│ AB│, 称作 : 向量的模 .AB2 . 小写字母表示法:用小写字母 , , …. 来表示。如图:abcabc 三、两个特殊向量:1. 零向量 :0记为长度等于1个单位的向量称为单位向量。长度等于0,方向任意的特殊向量。2. 单位向量:?平面直角坐标系中,起点在原点的单位向量,它们的终点的轨迹是什么图形?是单位向量有对任意向量||:,aaa 四、向量之间的关系:定义:长度相等且方向相同的向量称为相等向量。1. 相等向量ABCD平行四边形 ABCD 中:DCAB 说明:向量可以平移,因此向量又可称为自由向量。ab 2. 平行向量:规定:零向量与任何向量平行 .定义:方向相同或相反的非零向量。 平行向量又称为共线向量。3. 相反向量:规定:零向量的相反向量是零向量.定义:把与向量 a 长度相等、方向相反的向量叫做a 的相反向量,记为: a 与 -a 互为相反向量 .abc记作: // // a b c四、向量之间的关系: 例 1 :如图,设 O 是正六边形 ABCDEF 的中心,在如图所标出的向量中:(1) 试找出与 FE 共线的向量;(2) 确定与 FE 相等的向量;(3)OA 与 BC 相等吗?BCDEOFA解:⑴与 FE 共线的向量有 BC , OA .⑵BC 与 FE 长度相等且方向相同,故 BC=FE⑶ 虽然 OA∥BC ,且︱ OA ︱ = ︱ BC ︱,但它们方向相反,故这两个向量并不相等 . 问题 1 : OA = FE ? OB = AF ?问题 2 :是否存在与 OA 长度相等、方向相反的向量?问题 3 :与向量 OA 共线的向量有哪些?存在: FEAO 、 BC...