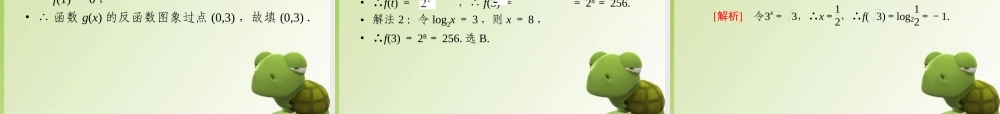• 阅读教材 P73 ,并完成下列各题:• 1 . 函 数 y = ax(a>0 且 a≠1) 与 函 数 互为反函数.y = logax(a>0 且 a≠1)• 3 .指数函数与对数函数性质对照表名称指数函数对数函数一般形式y = ax (a>0 ,且 a≠1)y = logax (a>0 ,且 a≠1)定义域( -∞,+∞ )(0 ,+∞ )值域(0 ,+∞ )( -∞,+∞ )单调性0
1时为单调增函数01 时为单调增函数.名称指数函数对数函数函数值变化情况名称指数函数对数函数图象y = ax 的图象与 y = logax 的图象关于直线 y = x 对称.底数变化情况第一象限内的图象所对应的指数函数的底数逆时针逐渐增大 .第一象限内的图象所对应的对数函数的底数逆时针逐渐减小 .• 4. 一般地,如果函数 y = f(x) 是一一对应的,则 y= f(x) 存在反函数,故单调 ( 严格 ) 函数一定存在反函数.• 求反函数时,将 y = f(x) 看作关于 x 的方程,解方程得 x = g(y) 改写为 y = g(x) 即得反函数,反函数的定义域和值域分别为原来函数的 和 .值域定义域• 5 .设 y = f(x) 存在反函数,并记作 y = f - 1(x) ,• (1) 如果点 P(x0 , y0) 在函数 y = f(x) 的图象上,则必有 f - 1(y0) =.• (2) 函数 y = f(x) 与其反函数 y = f - 1(x) 的图象关于直线 对称.• (3) 函数 y = f(x) 与其反函数 y = f - 1(x) 的单调性 .x0y = x相同• 本节重点:反函数的概念,互为反函数的两个函数的关系,指数函数与对数函数性质的比较.• 本节难点:互为反函数的两个函数的关系.• [ 例 1] 求函数 y = log2|x| 的定义域,并画出它的图象,由图象指出它的单调区间.• [ 分析 ] 可化为分段函数,利用函数图象的对称特征简化图象的作法.[解析] 函数的定义域为x≠0的一切实数,函数的解析式可化为y= log2x(x>0)log2(-x)(x<0) ,其图象如上图 由图象可知,此函数在(0,+∞)上是增函数,在(-∞,0)上是减函数. 画出函数 y=|log12x|的图象,求使|log12x|<1 成立的 x 的取值范围. [解析] 图象如图. |log12x|<1 化为-1