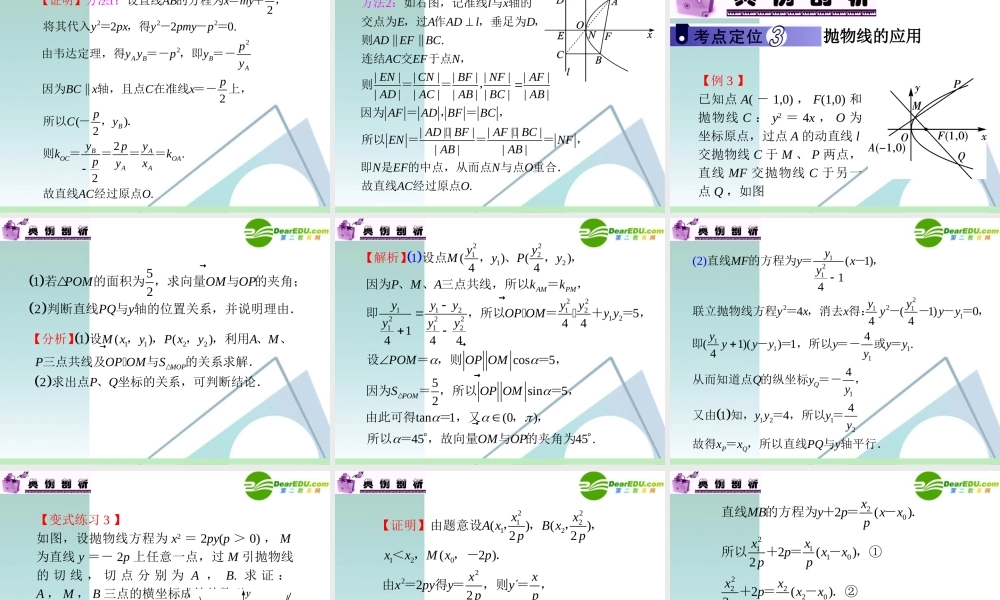
求抛物线的标准方程 【例 1 】求定点在原点,对称轴为坐标轴,且过点 ( - 3,2) 的抛物线的标准方程,并求对应抛物线的准线方程. 2222220(3,2)42(3)922293449321938ypxxpy pppppyxxyxy设所求的抛物线方程为 =-或 =.因为抛物线过点 -,所以 =-- 或 =,解得 = 或 =所以所求抛物线的方程为 =-或 =,对应的准线方程分别是 = ,解析=-【】 求抛物线的标准方程仅需确定一个待定系数 p. 从实际分析,一般需确定 p 和开口方向两个条件,有时需要相应的讨论. 【变式练习 1 】求顶点在原点,对称轴为坐标轴,且焦点在直线 x - 2y - 4 = 0 上的抛物线的标准方程,并求对应抛物线的准线方程. 220204.4,0(02)4,0482164(02)24282.xyyxppyxxppxyy令 = ,得 =- ;令 = ,得 =所以抛物线的焦点为或 ,- .当焦点为时, = ,所以 = ,此时抛物线的方程为 =,准线方程为 =- ;当焦点为 ,- 时, = ,所以 = ,此【时抛物线的方程为 =- ,准线方程为】=解析抛物线的几何性质 【例 2 】已知 A 、 B 是抛物线 y2 = 2px(p>0) 上的两点,且 OA⊥OB(O 为坐标原点 ) ,(1) 求证: A 、 B 这两点的横坐标之积为定值,纵坐标之积也是定值;(2) 求证:直线 AB 过定点;(3) 求线段 AB 中点 M 的轨迹方程. 11222211221212121222221212121221221212() ()2202244144ABxyxyypxypxOAOBx xy yx xy yy ypxpxp x xp y yy ypx xy yp证明:设 、 坐标分别为,, ,,则 =, =,因为,所以+= ,即=-,所以===-,所以=-为定值;=-=也【解析】是定值. 2212121212122112211221111212211211212121221212122()()222 ()222()()222242(2 )yyyyyypxpxp xxyypxxxxyyppyAByyxxxyyyyppypy yyxyxyyyyyyyypppxxpyyyyyy证明:因为=-+=-=-,又,所以=所以的方程为: - =-=-,所以 ==+=-所以直线2 ,0ABp过定点2211222212121212222222,22 ()()224842(2(3))ypx ypxyyp xxM xyyyyxxxyppxypxpyp xp因为所以=+,设, ,则 + = , + = ,所以+==-=-. p 的规律性结论很多,我们都可围绕定义,同时适时运用点差法即可求得.设 AB 为过抛物线 y2= ±2px(p>0) 焦点的弦,设 A(x1 , y1...