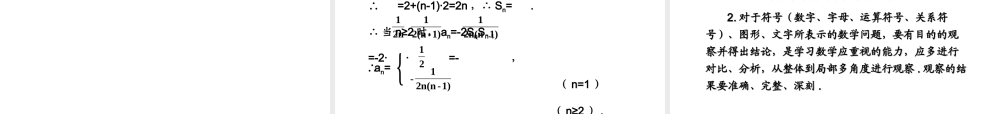数 列 数 列 考点考点 11考点考点 22填填知学情填填知学情课内考点突课内考点突破破规 律 探 究规 律 探 究考 纲 解 读考 纲 解 读考 向 预 测考 向 预 测知识网络构知识网络构建建 考 纲 解 读考 纲 解 读数列了解数列的概念和几种简单的表示方法 .了解数列是自变量为正整数的一类函数 . 从近两年的高考题来看 ,Sn 与 an 的关系 , 数列的递推公式是高考的热点 , 题型为解答题 , 分值在 12 分左右 , 属较难题目 , 旨在考查学生分析问题、解决问题的能力 . 在考查基本知识的同时又注重考查等价转化、函数与方程、分类讨论等思想方法 . 预测 2012 年高考仍将以 Sn 与 an 的关系为主要考点 , 重点考查学生的运算能力与逻辑推理能力 .考 向 预 测考 向 预 测 1. 按照 叫做数列 . 数列中的 叫做这个数列的项;在函数意义下,数列是定义域为 的函数, f ( n )是当自变量 n 从 1 开始依次取自然数时所对应的一列函数值 f( 1 ), f ( 2 ),…, f ( n ) ,…. 通常用 an 代替 f( n ),故数列的一般形式为: a1 , a2,a3,…,an,…, 简记为 {an}, 其中 an 是数列的第 项 .一定次序排列着的一列数 每一个数 N* 或它的子集 n 2. 如果数列 {an} 的 与序号 之间的关系可以用一个式子 an=f(n) 来表示 , 那么 an= f(n) 叫做数列的 .但并非每个数列都有通项公式 , 也并非都是唯一的 . 3. 如果已知数列 {an} 的第 项 ( 或 ), 且从第二项 ( 或某一项 ) 开始的 与它的 ( 或 ) 间的关系可以用一个公式来表示 , 那么这个公式叫数列的递推公式 . 数列常用的表示法有 :( 通项公式或递推公式 ) 、 、 .第 n 项 n 通项公式 1 前几项 任一项 an 前一项 an-1 前几项解析法 列表法 图象法 4. 数列按项数来分 , 分为 、 ;按项 增减规律分为 、 、 和 .递增数列 an+1 an; 递减数列 an+1 an; 常数列an+1 an. 递增数列与递减数列通称为 . 按任何一项的绝对值是否都小于某一正数来分,可分为 和 . ,( n=1 ) ,( n≥2 ) . an≥an-1, an≤an-1, an≥an+1. an≤an+1.Sn-Sn-1 5. 已知 Sn ,则 an= 数列 {an} 中,{{{若 an 最大,则若 an 最小,则⇔⇔⇔有穷数列 无穷数列 递增数列 递减数列 摆动数列 常数...