高中数学 第三讲 圆锥曲线性质的探讨课件 新人教A版选修4 1 课件VIP免费

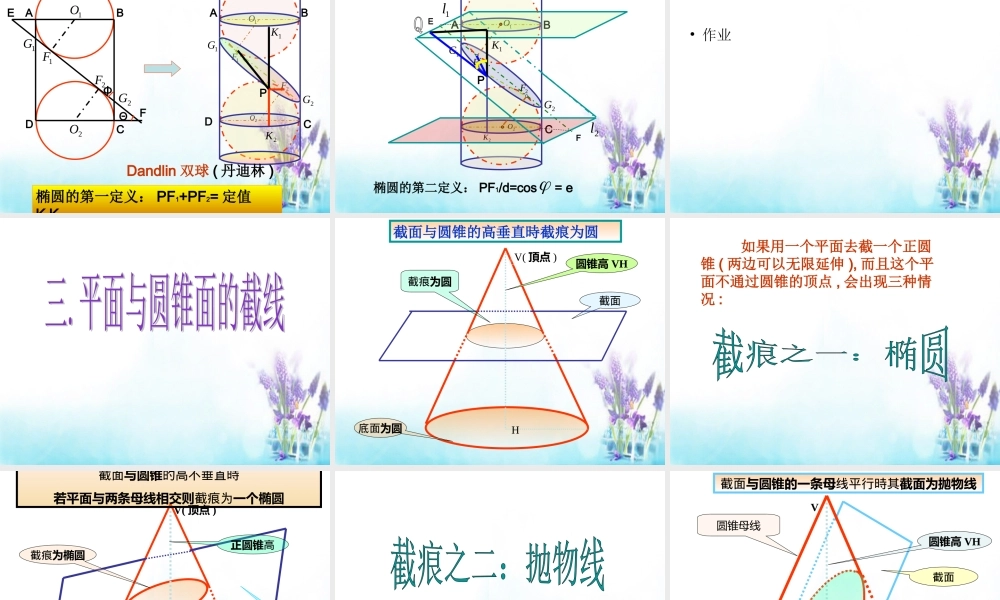
复习回顾点在直线上的正射影 线段在直线上的正射影 A´ANMNMABA´B´点在平面上的正射影 拓展延伸AA´图形在平面上的正射影 一个圆所在的平面 β 与平面 α 平行时，该圆在 α 上的正射影是什么图形？ 当 β 与 α 不平行时，圆在 α 上的正射影是什么图形 如果 β 与 α 垂直，圆在 α 上的正射影又是什么图形？思考：l平行射影的概念：直线 与平面 α 相交 ------ 的方向称投影方向。ll点的平行射影：过点 A 作平行于 的直线（称投影线）必交 α 于一点 A´, 称点 A´ 为 A 沿 的方 向在平面 α 上的平行射影。llAA 一个图形上各点在平面 α 上的平行射影所组成的图形，叫做这个图形的平行射影。正射影是平行射影的特例。图形的平行射影：思考：1. 两条相交直线的平行射影是否还是相交直线？2. 两条平行直线的平行射影是否还是平行直线？3. 将一个放在桌面上的玻璃杯中倒入半杯水，水面是一个圆；如果将玻璃杯倾斜一定角度呢？ABCFPEQGHDEF>AD EF>PQ定义：平面上到两个定点的距离之和等于定长的点的轨迹叫做椭圆。用一个平面去截一个圆柱，当平面与圆柱两底面平行时，截面是一个圆；当平面与两底面不平行时，截面是一个椭圆。二。平面与圆柱面的截线探究： 如图， AB,CD是两个等圆的直径， AB//CD, 均与两圆相切。作公切线 EF,切点分别为 交 BA,DC的延长线与 E,F, 交 AD 于 , 交 BC 于 ，设 EF与 BC,CD 的交角分别为 φ ， θ 。,,21 FF1G2GAEBDCF1F1O2O1G2G2FΦΘ• （ 1 ） G2F1+G2F2与AD 有什么关系？• （ 2 ） AD 的长与个G1G2的长有什么关系？• （ 3 ） G2F1与 G2E有什么关系？AEBDCF1F1O2O1G2G2FΦΘAD)1(2212FGFG21GGAD)2(AEBDCF1F1O2O1G2G2FΦΘAD222212BCCGBGFGFG ADAGDGCGDGGFDGGG?112122121.sin)90= cos(cos022212212 EGBGEGFGBGFG .sincos3212 EGFGAEBDCF1F1O2O1G2G2FΦΘ拓展到空间APBDC1F1O2O1G2G2F2K1KDandlin 双球 ( 丹迪林 )椭圆的第一定义： PF1+PF2= 定值K1K2APBC1F1O2O1G2G2F2K1K1l2lEF椭圆的第二定义： PF1/d=cos = e • 作业 底面为圆截痕为圆截面截面与圆锥的高垂直時截痕为圆V( 頂点 )H圆锥高 VH 如果用一个平面去截一个正圆锥 ( 两边可以无限延伸 ), 而且这个平面不通过圆锥的顶点 , 会出现三种情况 :底面为圆截面截痕...