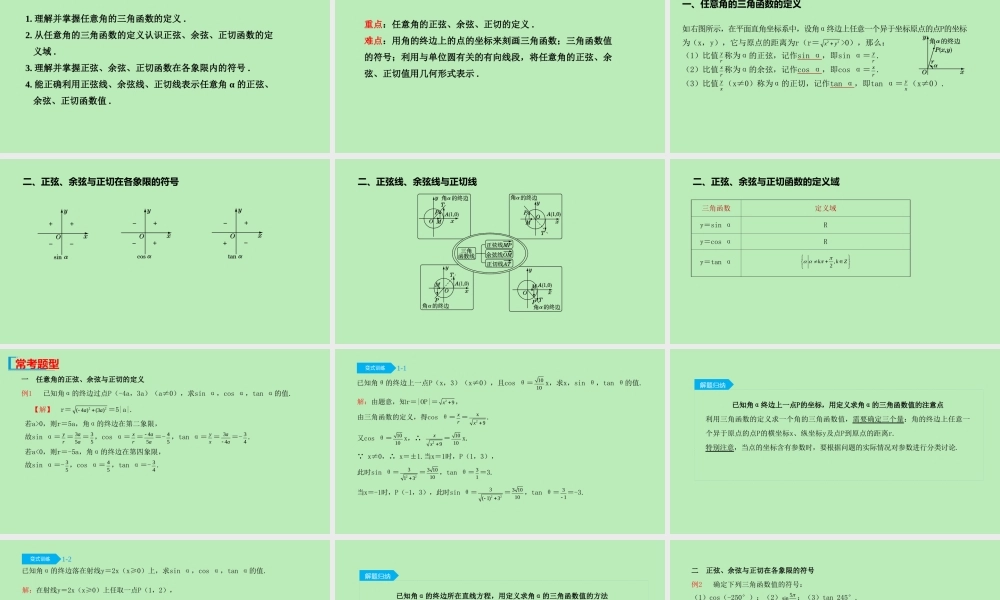
7.2 任意角的三角函数7.2.1 三角函数的定义7.2.2 单位圆与三角函数线第七章 三角函数学习目标1. 理解并掌握任意角的三角函数的定义 .2. 从任意角的三角函数的定义认识正弦、余弦、正切函数的定义域 .3. 理解并掌握正弦、余弦、正切函数在各象限内的符号 .4. 能正确利用正弦线、余弦线、正切线表示任意角 α 的正弦、余弦、正切函数值 .学习目标重点:任意角的正弦、余弦、正切的定义 .难点:用角的终边上的点的坐标来刻画三角函数;三角函数值的符号;利用与单位圆有关的有向线段,将任意角的正弦、余弦、正切值用几何形式表示 .知识梳理一、任意角的三角函数的定义 如右图所示,在平面直角坐标系中,设角α终边上任意一个异于坐标原点的点P的坐标为(x,y),它与原点的距离为r(r=22xy>0),那么: (1)比值 yr 称为α的正弦,记作sin α,即sin α= yr . (2)比值 xr 称为α的余弦,记作cos α,即cos α= xr . (3)比值 yx (x≠0)称为α的正切,记作tan α,即tan α= yx (x≠0). 二、正弦、余弦与正切在各象限的符号 二、正弦线、余弦线与正切线 二、正弦、余弦与正切函数的定义域 三角函数 定义域 y=sin α R y=cos α R y=tan α ,2kkZ 常考题型 【解】 r=22( 4 )(3 )aa=5|a|. 若a>0,则r=5a,角α的终边在第二象限, 故sin α= yr = 35aa = 35 ,cos α= xr = 45aa=- 45 ,tan α= yx = 34aa=- 34 . 若a<0,则r=-5a,角α的终边在第四象限, 故sin α=- 35 ,cos α= 45 ,tan α=- 34 . 一 任意角的正弦、余弦与正切的定义 例1 已知角α的终边过点P(-4a,3a)(a≠0),求sin α,cos α,tan α的值. 已知角θ的终边上一点P(x,3)(x≠0),且cos θ=1010 x,求x,sin θ,tan θ的值. 变式训练解:由题意,知r=|OP|=29x , 由三角函数的定义,得cos θ= xr =2x9x . 又cos θ=1010 x,∴ 29xx =1010 x. x≠0,∴ x=±1.当x=1时,P(1,3), 此时sin θ=22313= 3 1010 ,tan θ= 31 =3. 当x=-1时,P(-1,3),此时sin θ=223( 1)3= 3 1010 ,tan θ= 31 =-3. 1-1解题归纳已知角α终边上一点P的坐标,用定义求角α的三角函数值的注意点 利用三角函数的定义求一个角的三...