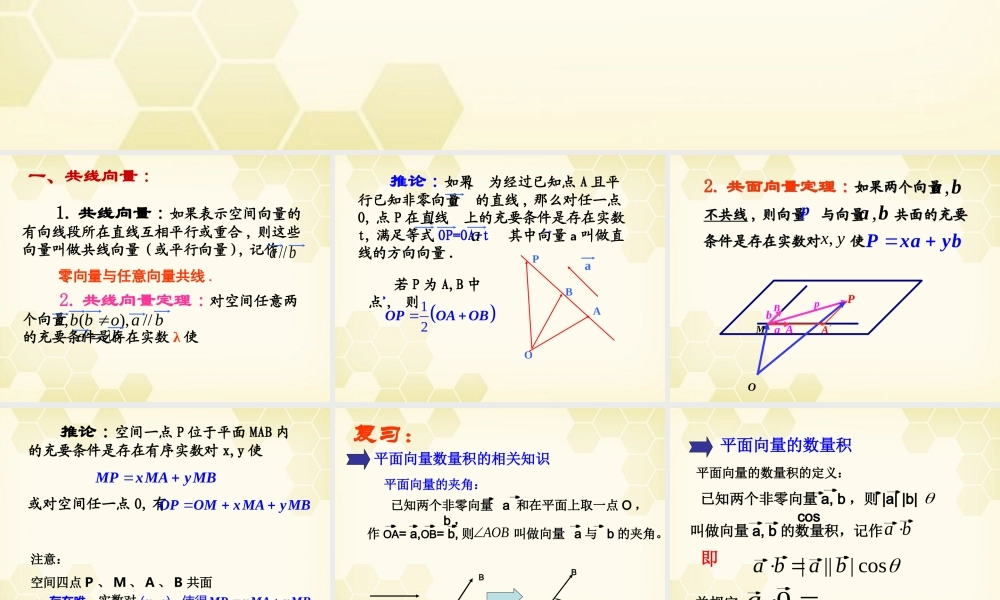
空间向量的数量积运算一、共线向量 :零向量与任意向量共线 . 1. 共线向量 : 如果表示空间向量的有向线段所在直线互相平行或重合 , 则这些向量叫做共线向量 ( 或平行向量 ), 记作 ba // 2. 共线向量定理 : 对空间任意两个向量 的充要条件是存在实数 λ 使baobba//),(,ba 推论 : 如果 为经过已知点 A 且平行已知非零向量 的直线 , 那么对任一点O, 点 P 在直线 上的充要条件是存在实数t, 满足等式 OP=OA+t 其中向量 a 叫做直线的方向向量 .llaaOABPa 若 P 为 A,B 中点 , 则 12�OPOAOB2. 共面向量定理 : 如果两个向量 不共线 , 则向量 与向量 共面的充要条件是存在实数对 使2. 共面向量定理 : 如果两个向量 不共线 , 则向量 与向量 共面的充要条件是存在实数对 使,a byx,�Pxayb�p,a bOMabABAPp� 推论 : 空间一点 P 位于平面 MAB 内的充要条件是存在有序实数对 x,y 使 或对空间任一点 O, 有 �MPxMAyMB�OPOMxMAyMB注意:空间四点 P 、 M 、 A 、 B 共面 存在唯一实数对,,xyMPxMAyMB�() 使得(1)OPxOMyOAzOBxyz�其中,平面向量数量积的相关知识复习: 平面向量的夹角:AOBAB叫做向量 a 与 b 的夹角。 已知两个非零向量 a 和 b ,在平面上取一点 O ,作 OA= a,OB= b, 则 AOB平面向量的数量积的定义:平面向量的数量积已知两个非零向量 a, b ,则 |a| |b|cos叫做向量 a, b 的数量积,记作ba即cos||||baba并规定 0 0a教学过程一、几个概念1 ) 两个向量的夹角的定义abbaba,,,0=被唯一确定了,并且量的夹角就在这个规定下,两个向范围:bababa互相垂直,并记作:与则称如果,2,OABaabb2 )两个向量的数量积注意: ①两个向量的数量积是数量,而不是向量 . ②零向量与任意向量的数量积等于零。babababababababaaaOAaOA,cos,,,cos,,,即记作:的数量积,叫做向量,则已知空间两个向量记作:的长度或模的长度叫做向量则有向线段设3 )射影eaeaABBAelABBABlBAlAllelaAB,cos,111111射影。方向上的正射影,简称或在上的在轴叫做向量,则上的射影在作点上的射影在点同方向的单位向量。作上与是,和轴=已知向量BAleA1B1注意: 是轴 l 上的正射影 ,A1B1 是一个可正...