高中数学 三角函数模型简单应用(一)课件 新人教A版 课件VIP免费

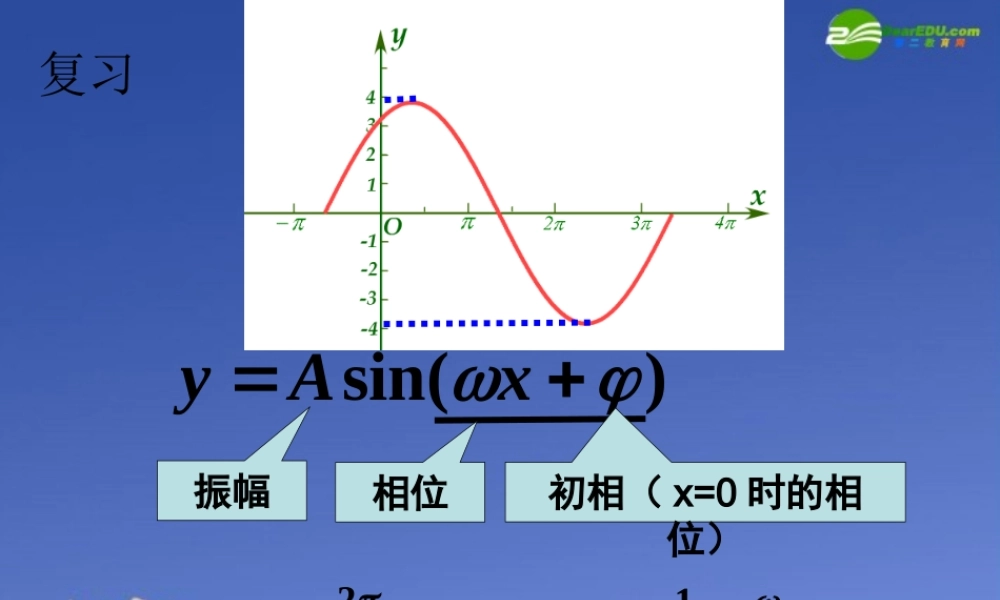
)sin( xAy振幅初相（ x=0 时的相位）相位2:T周期1:2fT频率复习1.6 三角函数模型的简单应用 第一课时 探究一：根据图象建立三角函数关系思考 1 ：这一天 6 ～ 14时的最大温差是多少？ 某地一天从 6 ～ 14时的温度变化曲线近似满足函数 :sin()yAxbT/℃102030ot/h6 10 14思考 2 ：函数式中 A 、b 的值分别是多少？30°-10°=20°A=10,b=20.【背景材料】如图，T/℃102030ot/h6 10 14sin()yAxb思考 3 ：如何确定函数式中 和 的值 ?w j3,84思考 4 ：这段曲线对应的函数是什么？3y10sin(x)20,x[6,14].84思考 5 ：这一天 12 时的温度大概是多少 （℃）？ 27.07℃. 圣米切尔山涨潮落潮【背景材料】 海水受日月的引力，在一定的时候发生涨落的现象叫潮 . 一般地，早潮叫潮，晚潮叫汐 . 在通常情况下，船在涨潮时驶进航道，靠近码头；卸货后，在落潮时返回海洋 . 下面是某港口在某季节每天的时间与水深关系表：52.557.552.557.55水深24211815129630时刻思考 1 ：观察表格中的数据，每天水深的变化具有什么规律性？呈周期性变化规律 .52.557.552.557.55水深24211815129630时刻52.557.552.557.55水深24211815129630时刻yo18246122468xyAsin( x)hA2.5,h5,T12,0,6 思考 5 ： 根据这个函数模型，求出各整点时水深的近似值吗？y2.5sinx563.7542.8352.5002.8353.7545.000水深23 ： 0022 ： 0021 ： 0020 ： 0019 ： 0018 ： 00时刻6.2507.1657.5007.1656.2505.000水深17 ： 0016 ： 0015 ： 0014 ： 0013 ： 0012 ： 00时刻3.7542.8352.5002.8353.7545.000水深11 ： 0010 ： 009 ： 008 ： 007 ： 006 ： 00时刻6.2507.1657.5007.1656.2505.000水深5 ： 004 ： 003 ： 002 ： 001 ： 000 ： 00时刻思考 6 ：一条货船的吃水深度（船底与水面的距离）为 4 米，安全条例规定至少要有 1.5 米的安全间隙（船底与洋底的距离），该船何时能进入港口？在港口能呆多久？ABCDyox246851015oxABCDy246851015每次可以在港口停留 5 小时左右 .0 时 30 分左右进港，早晨 5 时 30 分左右出港；或在中午 12 时 30 分左右进港，下午 17 时 30 分左右出港 .思考 7 ：若某船的吃水深度为 4 米，安全间隙为 1.5 米，该船在 2 ： 00 开始卸货，吃水深度以每小时 0.3 米的速度减少，那么该船在什么时间必须停止卸货，将船驶向较深的水域？y=-0.3x+6.1268 10 124xyo24682.5sin56yxp=+货船最好在 6.5 时之前停止卸货，将船驶向较深的水域 . 1. 分析数据；2. 画出散点图；3. 寻找数学模型；4. 解决实际问题。小结作业：P73 练习 :1 ， 2 ， 3.A 组 1 ， 2 ， 3预习： 68 页例 3