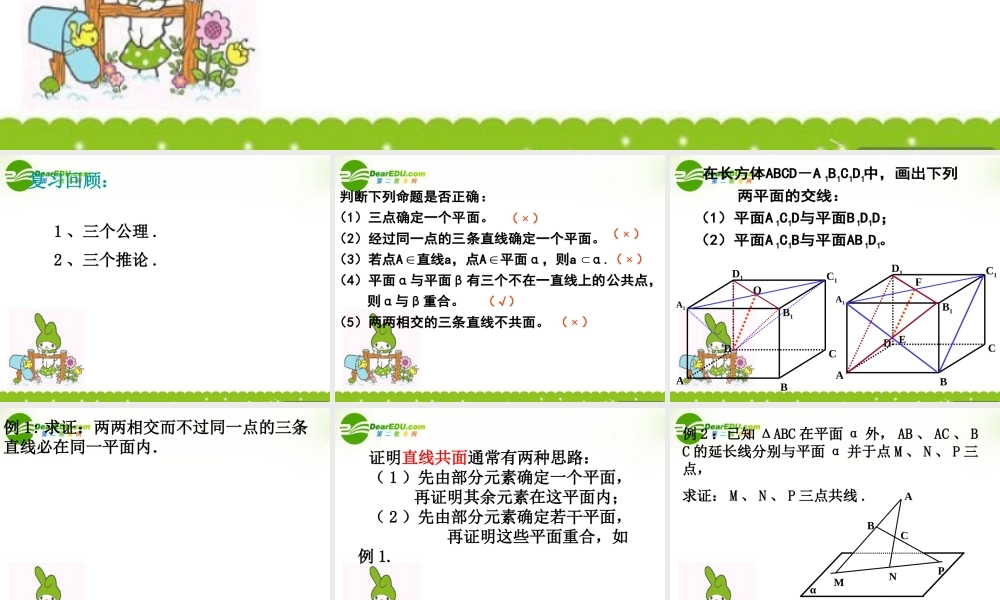
平面的基本性质(3 ) 复习回顾:1 、三个公理 .2 、三个推论 . 直线不共面。(5)两两相交的三条则α与β重合。公共点,有三个不在一直线上的(4)平面α与平面βα.平面α,则a直线a,点A(3)若点A条直线确定一个平面。(2)经过同一点的三面。(1)三点确定一个平:判断下列命题是否正确( × )( × )( × )(√)( × ) 。DB与平面ABC(2)平面AD;DD与平面BC(1)平面A两平面的交线:中,画出下列DCB在长方体ABCD-A111111111111ABCDA1B1C1D1OABCDA1B1C1D1EF 例 1: 求证:两两相交而不过同一点的三条直线必在同一平面内. 证明直线共面通常有两种思路:( 1 )先由部分元素确定一个平面, 再证明其余元素在这平面内;( 2 )先由部分元素确定若干平面, 再证明这些平面重合,如例 1. 例 2 :已知 ΔABC 在平面 α 外, AB 、 AC 、 BC 的延长线分别与平面 α 并于点 M 、 N 、 P 三点,求证: M 、 N 、 P 三点共线 .αBACMNP 证明三点共线通常先确定经过两点的直线是某两个平面的交线,再证明第三点是这两个平面的公共点,即该点分别在这两个平面内,如例 2. 例 3: 三个平面两两相交,有三条交线,若其中两条相交于一点,证明第三条交线也过这一点. 已知 :求证 : 证明三线共点通常先证其中的两条直线相交于一点,然后再证第三条直线经过这一点,如例 3. //// ,,,abc alA blB clCabcd1、已知:求证: 、 、 、 共面练习:11111111111112..ABCDA B C DOA CB DA CB D APOPA、已知长方体中,是上地面对角线、的交点,体对角线交截面于点求证:、 、 三点在同一直线上3:2 : 3,:2 : 3..ABCDEGBCABFCDHADDF FCDHHAEFGHBD、四面体中, 、 分别为、中点, 在上,在上,且有求证:、、交于一点 小结:掌握利用平面的基本性质证明诸点共面、诸线共面、三点共线、三线共点问题的一般方法.1 .证明若干点或直线共面通常有两种思路( 1 )先由部分元素确定若干平面,再证明这些平面重合;( 2 )先由部分元素确定一个平面,再证明其余元素在这 平面内.2 .证明三点共线,通常先确定经过两点的直线是某两个 平面的交线,再证明第三点是这两个平面的公共点, 即该点分别在这两个平面内.3 .证明三线共点,通常先证其中的两条直线相交于一点, 然后再证第三条直线经过这一点.