高中数学 151函数y=Asinωxφ的图象一课件 新人教A版必修4 课件VIP免费

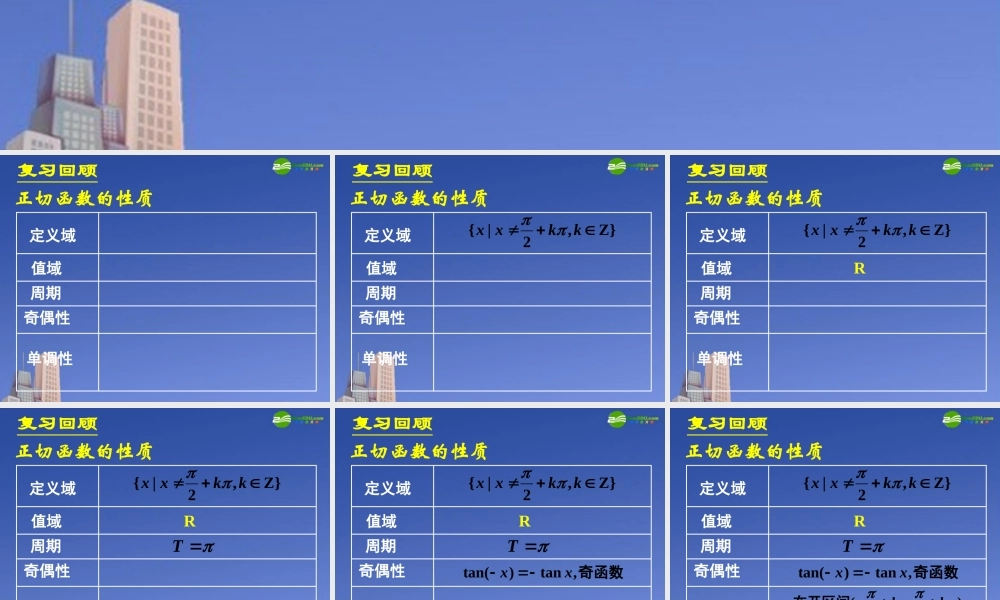
1.5 函数 y=Asin(x+)的图象 复习回顾正切函数的性质定义域值域周期奇偶性单调性定义域}Z,2|{kkxx值域周期奇偶性单调性复习回顾正切函数的性质定义域}Z,2|{kkxx值域R周期奇偶性单调性复习回顾正切函数的性质定义域}Z,2|{kkxx值域R周期T奇偶性单调性复习回顾正切函数的性质定义域}Z,2|{kkxx值域R周期T奇偶性奇函数,tan)tan(xx单调性复习回顾正切函数的性质定义域}Z,2|{kkxx值域R周期T奇偶性奇函数,tan)tan(xx单调性内，函数单调递增在开区间Z)2,2(kkk复习回顾正切函数的性质练习 1. 求函数33tanxy值域，指出它的周期性、单调性 . 的定义域、复习回顾33tanxy值域，指出它的周期性、单调性 . 的定义域、思考：你能判断它的奇偶性吗？ 练习 1. 求函数复习回顾33tanxy值域，指出它的周期性、单调性 . 的定义域、思考：你能判断它的奇偶性吗？ 非奇非偶函数练习 1. 求函数复习回顾.32tan单调性域、周期性、奇偶性、的定义求函数 xy练习 2. 复习回顾思考：你能用图象求函数 tan3yx3tanxy的定义域吗 ?复习回顾tan3yx讲授新课1. “ 五点法”作函数 y=sinx 简图的步骤， 其中“五点”是指什么？2. f(x ＋ k) 的图象与 f(x) 的图象有什么样 的关系？tan3yx讲授新课1. “ 五点法”作函数 y=sinx 简图的步骤， 其中“五点”是指什么？2. f(x ＋ k) 的图象与 f(x) 的图象有什么样 的关系？)0,2( ),1,23( ),0,( ),1,2( ),0,0(tan3yx讲授新课1. 函数 y ＝ sin(x±)( ＞ 0) 的图象和函数y ＝ sinx 图象的关系是什么？思考 tan3yx讲授新课1. 函数 y ＝ sin(x±)( ＞ 0) 的图象和函数y ＝ sinx 图象的关系是什么？思考 函数 y ＝ sin(x±)(>0) 的图象可由函数 y ＝ sinx 的图像向左 ( 或右 ) 平移个单位而得到，tan3yx讲授新课1. 函数 y ＝ sin(x±)( ＞ 0) 的图象和函数y ＝ sinx 图象的关系是什么？思考 函数 y ＝ sin(x±)(>0) 的图象可由函数 y ＝ sinx 的图像向左 ( 或右 ) 平移个单位而得到，这种变换实际上是纵坐标不变，横坐标增加 ( 或减少 ) 个单位，这种变换称为平移变换 .tan3yx讲授...