高一数学向量的加法课件 北师大版 必修4 1 课件VIP免费

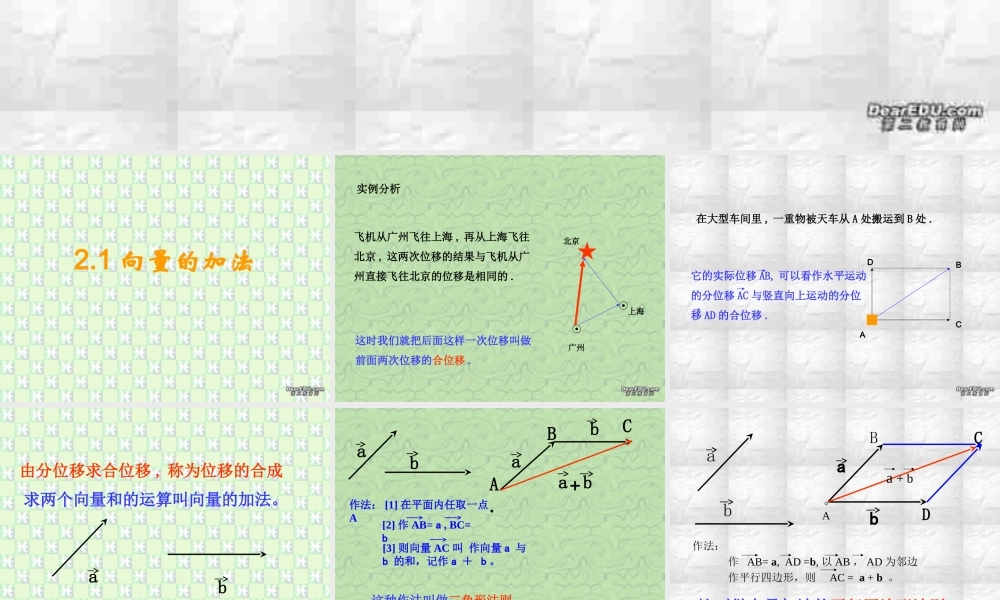
2.1 向量的加法北京广州上海实例分析飞机从广州飞往上海 , 再从上海飞往北京 , 这两次位移的结果与飞机从广州直接飞往北京的位移是相同的 .这时我们就把后面这样一次位移叫做前面两次位移的合位移 .AB在大型车间里 , 一重物被天车从 A 处搬运到 B 处 .它的实际位移 AB, 可以看作水平运动的分位移 AC 与竖直向上运动的分位移 AD 的合位移 .CD由分位移求合位移 , 称为位移的合成求两个向量和的运算叫向量的加法。ab这种作法叫做三角形法则abA.BaCb作法： [1] 在平面内任取一点A[2] 作 AB= a , BC= b[3] 则向量 AC 叫 作向量 a 与 b 的和，记作 a ＋ b 。ba+这叫做向量加法的平行四边形法则。作法： 作 AB= a, AD =b, 以 AB ， AD 为邻边 作平行四边形，则 AC = a + b 。abAaBbDCa + b 共线向量求和ab方向相同ab方向相反CBAbaACbaACABC例１轮船从Ａ港沿东偏北 方向行驶了40 海里到达 B 处 , 再由 B 处沿正北方向行驶 40 海里到达 C 处 . 求此时轮船与 A 港的相对位置 .30东北AB30C。轮船的合位移表示则移分别表示轮船的两次位、解：如图，设CCBABAC，AC，BABmilen 320||，milen 20||milen 40||,30,90,ADDBABADBADBADBRt所以，中△在。 所以，中△在60||2||milen 34060)320(||||||milen 60||,90,2222CADADACDCADACDCADCADCRtD向量的加法满足① 交换律： a + b = b + a② 结合律：（ a + b ) + c = a + ( b + c )cbaAaBCbDc例 2 两个力 F1 和 F2 同时作用在一个物体上 , 其中 F1 =40N, 方向向东 ,F2=30N, 方向向北 , 求它们的合力 .东北OBθCF。OCOACB，OAA， ，FOB，FOA表示合力则平行四边形为邻边作以表示表示解：如图，.21NACOAOCFOBACFOAOACRt503040||||||F，N. 30||||N 40||,222221得由勾股定理，中△在ＡＢF1F2375075.043||||tan121方向向东偏北合力大小为所以则的夹角为与设合力N，，FFOAAC，FF例 3 在小船过河时 , 小船沿垂直河岸方向行驶的速度为 v1=3.46km/h ，河水流动的速度 v2=2.0km/h ，试求小船过河实际航行速度的大小和方向 .。就是船实际航行的速度，则为邻边作平行四边形、表示水流的速度，以驶的速度表示船向垂直于对岸行解：如图，设OCABCDOBOAOBOA...