高中数学 点到直线的距离与平行直线间的距离课件 新人教B版必修2 课件VIP免费

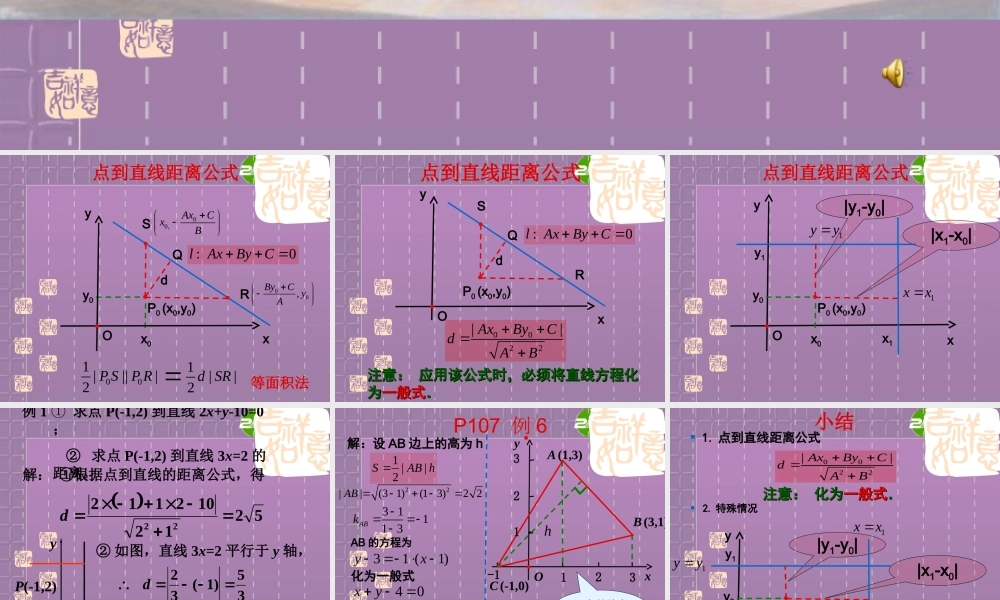
读书改变命运 素质成就未来 3.3.3 点到直线的距离 3.3.4 两条平行直线间的距离 点到直线距离公式xyP0 (x0,y0)Ox0y0:0lAxByCS00,AxCxBR00,ByC yA001 ||||2 P SP RQd1||2 d SR等面积法 点到直线距离公式xyP0 (x0,y0)O:0lAxByCSR0022||AxByCdABQd注意：注意： 应用该公式时，必须将直线方程化应用该公式时，必须将直线方程化为为一般式一般式．． 点到直线距离公式xyP0 (x0,y0)O|x1-x0||y1-y0|x0y01yyy11xxx1 例 1 ① 求点 P(-1,2) 到直线 2x+y-10=0； ② 求点 P(-1,2) 到直线 3x=2 的距离。解： ①根据点到直线的距离公式，得521210211222d② 如图，直线 3x=2 平行于 y 轴，Oyxl:3x=2P(-1,2)35)1(32d用公式验证，结果怎样 ? ？ P107 例 61 ||2SAB h解：设 AB 边上的高为 h22||(3 1)(1 3)2 2AB 3 111 3ABkAB 的方程为xyC (-1,0) O-1122331B (3,1)A (1,3)h31 (1)yx 化为一般式40xy22| 1 04 |11h  152 2522S  还有其他方法吗？ 小结 1. 点到直线距离公式 2. 特殊情况0022||AxByCdAB注意：注意： 化为化为一般式一般式．． xyP0 (x0,y0)O|x1-x0||y1-y0|x0y01yyy11xxx1 例 2 求平行线 2x-7y+8=0 与 2x-7y-6=0 的距离。Oyxl2: 2x-7y-6=0l1:2x-7y+8=0 P(3,0)两平行线间的距离处处相等在 l2 上任取一点，例如 P(3,0)P 到 l1 的距离等于 l1 与 l2 的距离5353145314)7(28073222d直线到直线的距离转化为点到直线的距离 Oyxl2l1PQ任意两条平行直线都可以写成如下形式：l1 :Ax+By+C1=0l2 :Ax+By+C2=0PQ 2212BACC 例 3 、求直线 3x+4y=10 和直线 6x+8y=3 之间的距离。 要求：1. 理解点到直线的距离公式的推导过程；2. 能用点到直线的距离公式进行计算；3. 能求有关平行线间的距离。思考题：直线 l 在两坐标轴上的截距相等，点 P(4,3) 到 l 的距离为 3 ，求直线 l 的方程。2