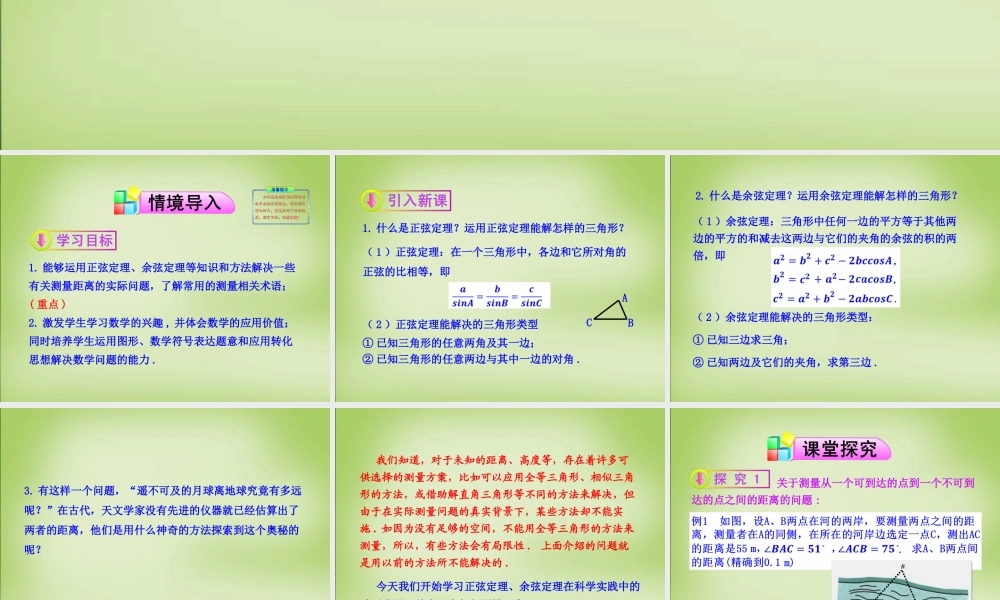
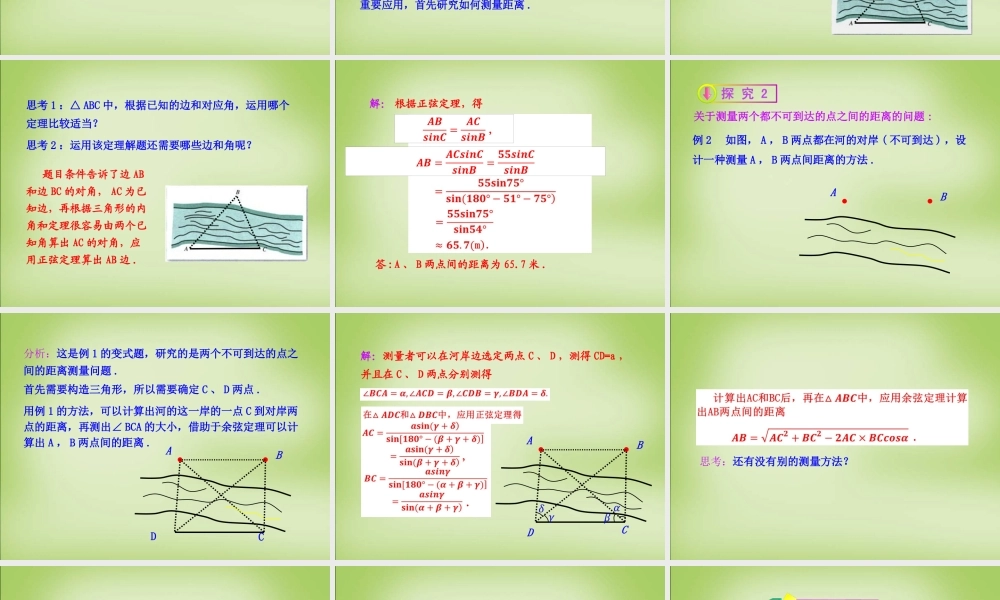
第 1 课时 解三角形的实际应用举例— 距离问题1.2 应用举例1. 能够运用正弦定理、余弦定理等知识和方法解决一些有关测量距离的实际问题,了解常用的测量相关术语;( 重点 )2. 激发学生学习数学的兴趣 , 并体会数学的应用价值;同时培养学生运用图形、数学符号表达题意和应用转化思想解决数学问题的能力 .BCA1. 什么是正弦定理?运用正弦定理能解怎样的三角形?( 1 )正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,即 ② 已知三角形的任意两边与其中一边的对角 . ( 2 )正弦定理能解决的三角形类型① 已知三角形的任意两角及其一边; 2. 什么是余弦定理?运用余弦定理能解怎样的三角形?( 1 )余弦定理:三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍,即① 已知三边求三角;( 2 )余弦定理能解决的三角形类型:② 已知两边及它们的夹角,求第三边 .3. 有这样一个问题,“遥不可及的月球离地球究竟有多远呢?”在古代,天文学家没有先进的仪器就已经估算出了两者的距离,他们是用什么神奇的方法探索到这个奥秘的呢?我们知道,对于未知的距离、高度等,存在着许多可供选择的测量方案,比如可以应用全等三角形、相似三角形的方法,或借助解直角三角形等不同的方法来解决,但由于在实际测量问题的真实背景下,某些方法却不能实施 . 如因为没有足够的空间,不能用全等三角形的方法来测量,所以,有些方法会有局限性 . 上面介绍的问题就是用以前的方法所不能解决的 .今天我们开始学习正弦定理、余弦定理在科学实践中的重要应用,首先研究如何测量距离 . 关于测量从一个可到达的点到一个不可到达的点之间的距离的问题 :思考 2 :运用该定理解题还需要哪些边和角呢?思考 1 :△ ABC 中,根据已知的边和对应角,运用哪个定理比较适当?题目条件告诉了边 AB和边 BC 的对角, AC 为已知边,再根据三角形的内角和定理很容易由两个已知角算出 AC 的对角,应用正弦定理算出 AB 边 .根据正弦定理,得答 :A 、 B 两点间的距离为 65.7 米 .解:,.关于测量两个都不可到达的点之间的距离的问题 :例 2 如图, A , B 两点都在河的对岸 ( 不可到达 ) ,设计一种测量 A , B 两点间距离的方法 .AB分析:这是例 1 的变式题,研究的是两个不可到达的点之间的距离测量问题 .AB首先需要构造三角形,所以需要确定 C 、 D ...