高中数学 232平面与平面垂直的判定课件 新人教B版必修2 课件VIP免费

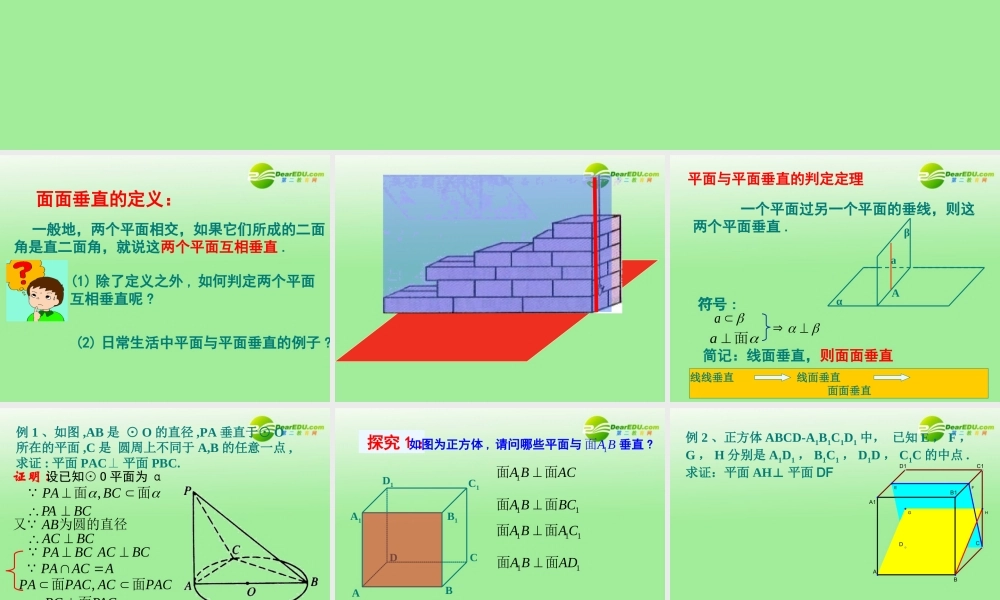
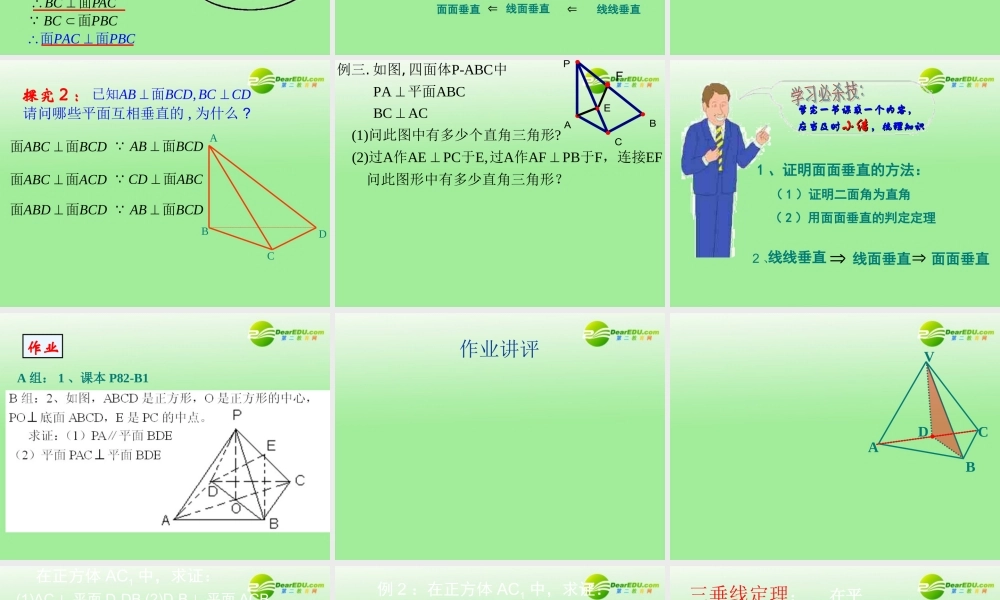
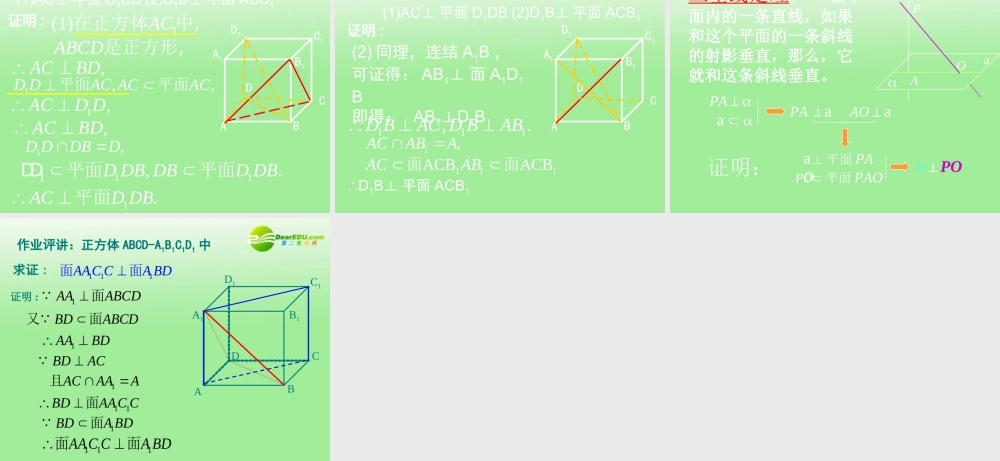
一般地，两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直 .面面垂直的定义：(2) 日常生活中平面与平面垂直的例子 ?(1) 除了定义之外 , 如何判定两个平面互相垂直呢 ?平面与平面垂直的判定定理 一个平面过另一个平面的垂线，则这两个平面垂直 .符号 :αβaA简记：线面垂直，则面面垂直 面面垂直线面垂直线线垂直aa 面 符号 :例 1 、如图 ,AB 是 ⊙ O 的直径 ,PA 垂直于⊙ O所在的平面 ,C 是 圆周上不同于 A,B 的任意一点 ,求证 : 平面 PAC⊥ 平面 PBC. 证明 :设已知⊙ O 平面为 α,PABC面面BCPA 为圆的直径又ABBCAC PAACAPACBC面PACPBC面面BCPBC面PABCACBC,PAPAC ACPAC面面探究 1 ：ACBDA1C1B1D1如图为正方体 , 请问哪些平面与 垂直 ?1A BAC面面11BCBA面面111CABA面面11ADBA面面面面垂直线面垂直线线垂直1A B面例 2 、正方体 ABCD-A1B1C1D1 中， 已知 E ， F ，G ， H 分别是 A1D1 ， B1C1 ， D1D ， C1C 的中点 .求证：平面 AH⊥ 平面 DFHFGED1C1B1DCBAA1,ABBCD BCCD已知面请问哪些平面互相垂直的 , 为什么 ?BCDABC面面ACDABC面面BCDABD面面BCDAB面ABCCD面BCDAB面探究 2 ：ABCDP-ABCPAABCBCAC (1)? 例三. 如图, 四面体中 平面 问此图中有多少个直角三角形 (2)AAEPCE,AAFPBFEF 过 作于过 作于 ，连接问此图形中有多少直角三角形？ABCPEF1 、证明面面垂直的方法： （ 1 ）证明二面角为直角（ 2 ）用面面垂直的判定定理2 、面面垂直线面垂直线线垂直学完一节课或一个内容，学完一节课或一个内容，应当及时应当及时小结小结，梳理知识，梳理知识作业A 组： 1 、课本 P82-B1作业讲评 VCABD在正方体 AC1 中，求证：(2)D1B⊥ 平面 ACB1(1)AC⊥ 平面 D1DBC1BD1ACA1DB1证明 :ABCD是正方形,,ACBD1,D DAC 平面1 ,ACD D1,D DDBD1.ACD DB 平面,ACAC平面,ACBD11,.D DB DBD DB1DD平面平面1(1)AC在正方体中,例 2 ：在正方体 AC1 中，求证：(2)D1B⊥ 平面 ACB1(1)AC⊥ 平面 D1DBC1BD1ACA1DB1证明 :(2) 同理，连结 A1B ，可证得： AB1⊥ 面 A1D1B即得： AB1D⊥1B111,.D BAC D BAB1,ACABA∴D1B⊥ 平面 ACB1111ACBACBACAB面面三垂线定理 ：在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么，它就和这条斜线垂直。AaOP证明：a⊥POPA⊥ a  AO⊥aa⊥ 平面 PAOPO 平面 PAOPA ⊥a作业评讲：正方体 ABCD-A1B1C1D1 中 求证 :111AAC CA BD面面证明 :1AAABCD面ABCDBD面又1AABDBDAC1ACAAA且11BDAAC C 面1BDA BD面111AAC CA BD面面ACBDA1C1B1D1