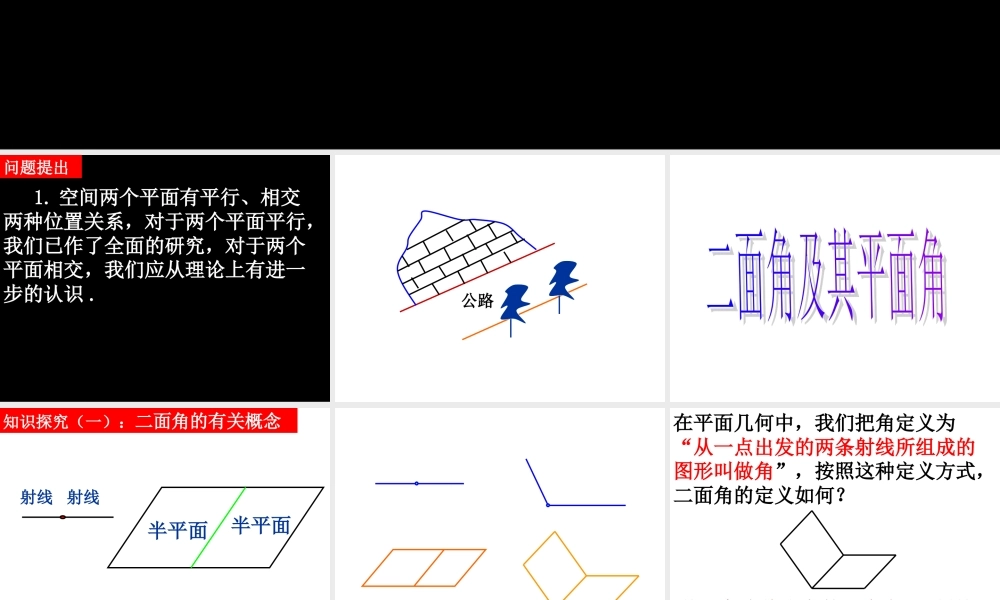
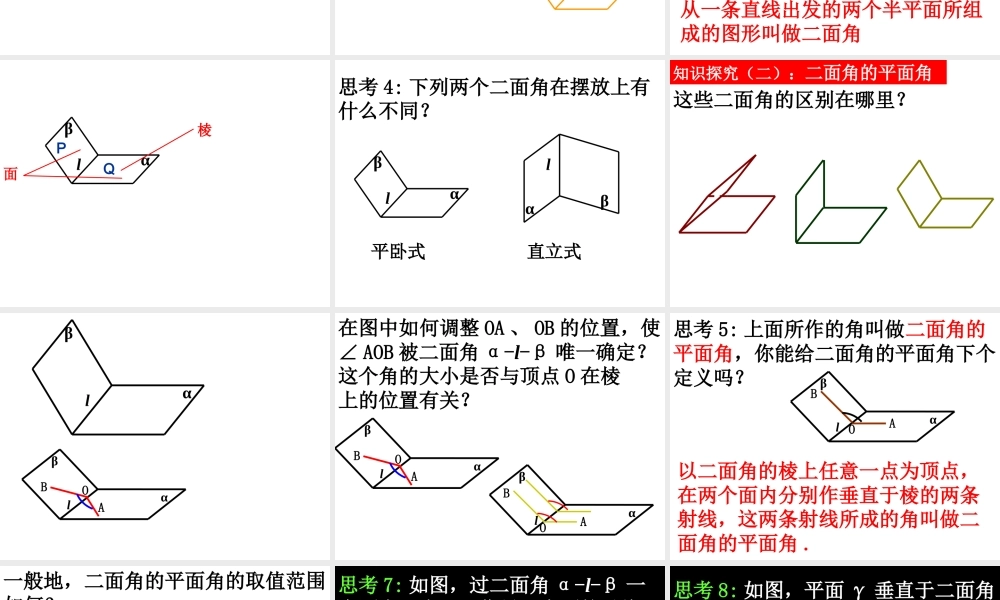
2.3.2 平面与平面垂直的判定 第一课时二面角的有关概念 问题提出 1. 空间两个平面有平行、相交两种位置关系,对于两个平面平行,我们已作了全面的研究,对于两个平面相交,我们应从理论上有进一步的认识 . 公路 知识探究(一):二面角的有关概念 半平面半平面射线射线 在平面几何中,我们把角定义为“从一点出发的两条射线所组成的图形叫做角”,按照这种定义方式,二面角的定义如何?从一条直线出发的两个半平面所组成的图形叫做二面角 lαβ棱面PQ 思考 4: 下列两个二面角在摆放上有什么不同?lαβαβl平卧式直立式 知识探究(二):二面角的平面角 这些二面角的区别在哪里? lαβlαβOAB 在图中如何调整 OA 、 OB 的位置,使∠ AOB 被二面角 α-l-β 唯一确定?lαβOABlαβOAB这个角的大小是否与顶点 O 在棱上的位置有关? 思考 5: 上面所作的角叫做二面角的平面角,你能给二面角的平面角下个定义吗?以二面角的棱上任意一点为顶点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角 .lαβOAB 一般地,二面角的平面角的取值范围如何?[0 ,180 ] 思考 7: 如图,过二面角 α-l-β 一个面内一点 A ,作另一个面的垂线,垂足为 B ,过点 B 作棱的垂线,垂足为 O ,连结 AO ,则∠ AOB 是二面角的平面角吗?为什么?ABOlαβ 思考 8: 如图,平面 γ 垂直于二面角的棱 l ,分别与面 α 、 β 相交于 OA 、OB ,则∠ AOB 是二面角的平面角吗?为什么?αβlAOBγαβ 理论迁移 例 1 在正方体 ABCD-A1B1C1D1 中,求二面角 B1-AC-B 大小的正切值 .AA1BCDB1C1D1O 60例 2 如图所示,河堤斜面与水平面所成二面角为 ,堤面上有一条直道 CD ,它与堤角的水平线 AB 的夹角为 ,沿这条直道从堤脚 C 向上行走10m 到达 E 处,此时人升高了多少 m ?ABCDE6030OF 作业 :P73 习题 2.3 A 组: 4 ,7.