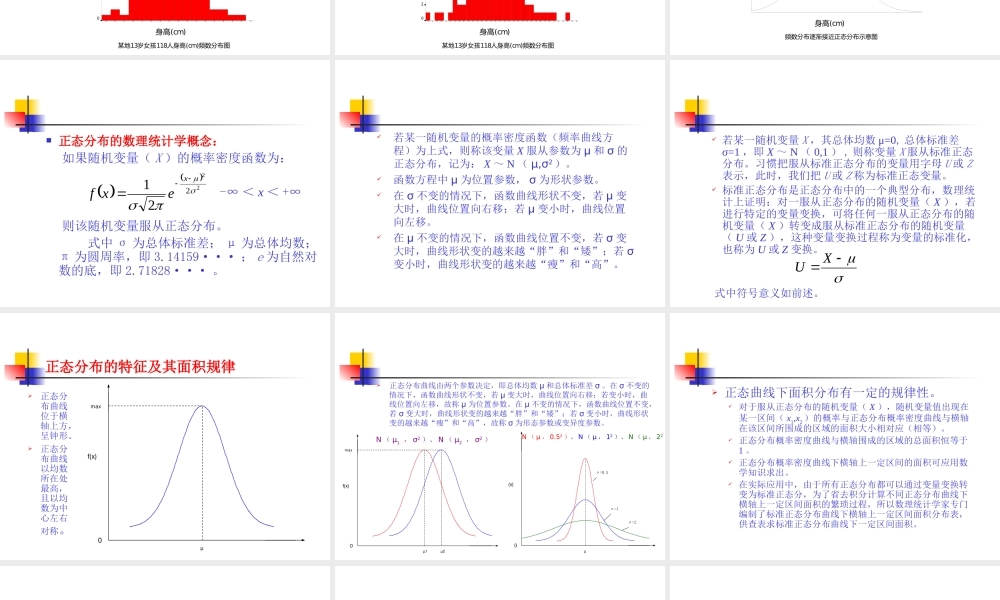
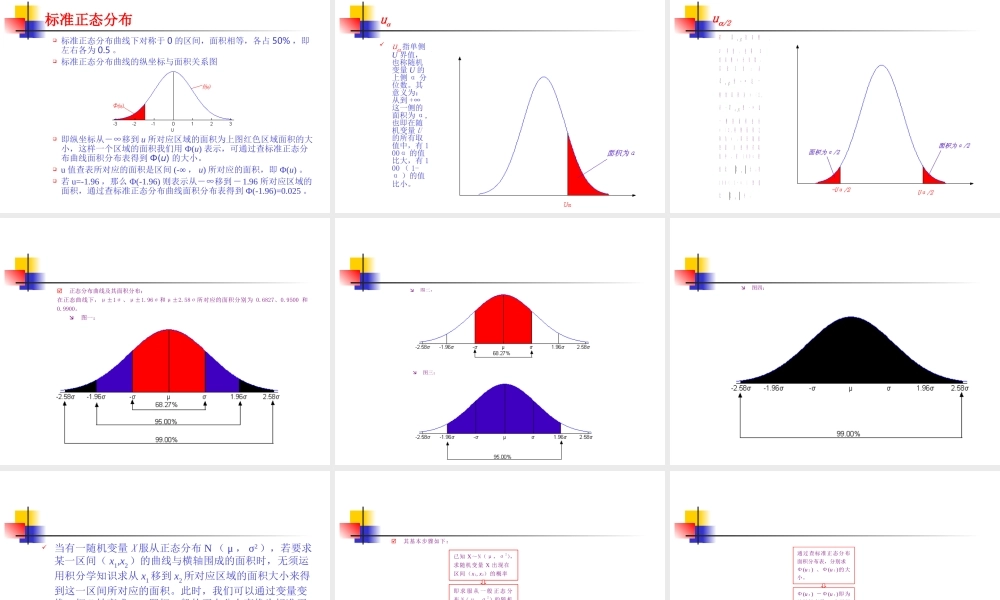
正态分布 正态分布的通俗概念: 如果把数值变量资料编制频数表后绘制频数分布图(又称直方图,它用矩形面积表示数值变量资料的频数分布,每条直条的宽表示组距,直条的面积表示频数(或频率)大小,直条与直条之间不留空隙。),若频数分布呈现中间为最多,左右两侧基本对称,越靠近中间频数越多,离中间越远,频数越少,形成一个中间频数多,两侧频数逐渐减少且基本对称的分布,那我们一般认为该数值变量服从或近似服从数学上的正态分布。正态分布的概念 下面我们以第一节某地 13 岁女孩 118 人的身高 (cm) 资料,来说明身高变量服从正态分布。频数分布表:某地 13 岁女孩 118 人的身高(cm)资料频数分布 身高组段 频数 组中值 (1) (2) (3) 129~ 2 130.5 132~ 2 133.5 135~ 8 136.5 138~ 20 139.5 141~ 26 142.5 144~ 25 145.5 147~ 20 148.5 150~ 9 151.5 153~ 3 154.5 156~ 2 157.5 159~162 1 160.5 合计 118 — 频数分布图一(又称直方图) (cm)身高160.5157.5154.5151.5148.5145.5142.5139.5136.5133.5130.5 13118(cm)某地岁女孩人身高频数分布图频数3020100从频数表及频数分布图上可得知: 该数值变量资料频数分布呈现中间频数多,左右两侧基本对称的分布。所以我们通俗地认为该资料服从正态分布。 (cm)身高 13118(cm)某地岁女孩人身高频数分布图频数20100频数分布图二 频数分布图三(cm)身高 13118(cm)某地岁女孩人身高频数分布图频数14121086420 正态分布图四(cm)身高 频数分布逐渐接近正态分布示意图 正态分布的数理统计学概念: 如果随机变量( X )的概率密度函数为: -∞ < x < +∞ 则该随机变量服从正态分布。 式中 σ 为总体标准差; μ 为总体均数;π 为圆周率,即 3.14159··· ; e 为自然对数的底,即 2.71828··· 。 22221xexf 若某一随机变量的概率密度函数(频率曲线方程)为上式,则称该变量 X 服从参数为 μ 和 σ 的正态分布,记为: X ~ N ( μ,σ2)。函数方程中 μ 为位置参数, σ 为形状参数。在 σ 不变的情况下,函数曲线形状不变,若 μ 变大时,曲线位置向右移;若 μ 变小时,曲线位置向左移。在 μ 不变的情况下,函数曲线位置不变,若 σ 变大时,曲线形状变的越来越“胖”和“矮”;若 σ变小时,曲线形状变的越来越...