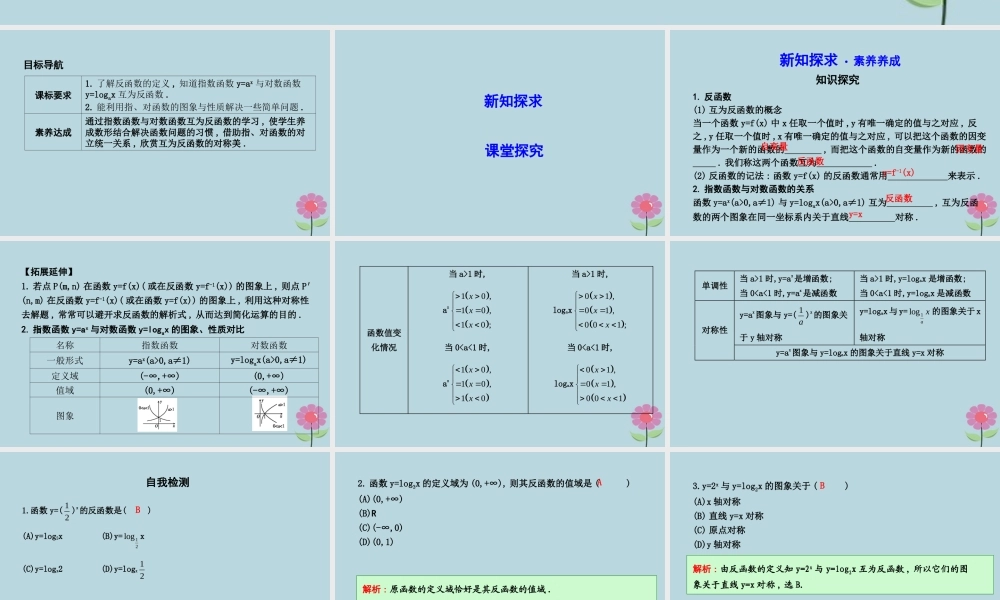
3.2.3 指数函数与对数函数的关系目标导航课标要求1. 了解反函数的定义 , 知道指数函数 y=ax 与对数函数y=logax 互为反函数 .2. 能利用指、对函数的图象与性质解决一些简单问题 .素养达成通过指数函数与对数函数互为反函数的学习 , 使学生养成数形结合解决函数问题的习惯 , 借助指、对函数的对立统一关系 , 欣赏互为反函数的对称美 .新知探求课堂探究新知探求 · 素养养成知识探究1. 反函数(1) 互为反函数的概念当一个函数 y=f(x) 中 x 任取一个值时 ,y 有唯一确定的值与之对应 , 反之 ,y 任取一个值时 ,x 有唯一确定的值与之对应 , 可以把这个函数的因变量作为一个新的函数的 , 而把这个函数的自变量作为新的函数的 . 我们称这两个函数互为 .(2) 反函数的记法 : 函数 y=f(x) 的反函数通常用 来表示 .2. 指数函数与对数函数的关系函数 y=ax(a>0,a≠1) 与 y=logax(a>0,a≠1) 互为 , 互为反函数的两个图象在同一坐标系内关于直线 对称 .自变量因变量反函数y=f-1(x)反函数y=x【拓展延伸】1. 若点 P(m,n) 在函数 y=f(x)( 或在反函数 y=f-1(x)) 的图象上 , 则点 P′(n,m) 在反函数 y=f-1(x)( 或在函数 y=f(x)) 的图象上 , 利用这种对称性去解题 , 常常可以避开求反函数的解析式 , 从而达到简化运算的目的 .2. 指数函数 y=ax 与对数函数 y=logax 的图象、性质对比名称指数函数对数函数一般形式y=ax(a>0,a≠1)y=logax(a>0,a≠1)定义域(-∞,+∞)(0,+∞)值域(0,+∞)(-∞,+∞)图象函数值变 化情况 当 a>1 时, ax10 ,10 ,10 ;xxx 当 0
1 时, logax01 ,01 ,0 01 ;xxx 当 01 时,y=ax是增函数; 当 01 时,y=logax 是增函数; 当 0