高中数学 1313 正弦型函数的图象课件 新人教B版必修4 课件VIP免费

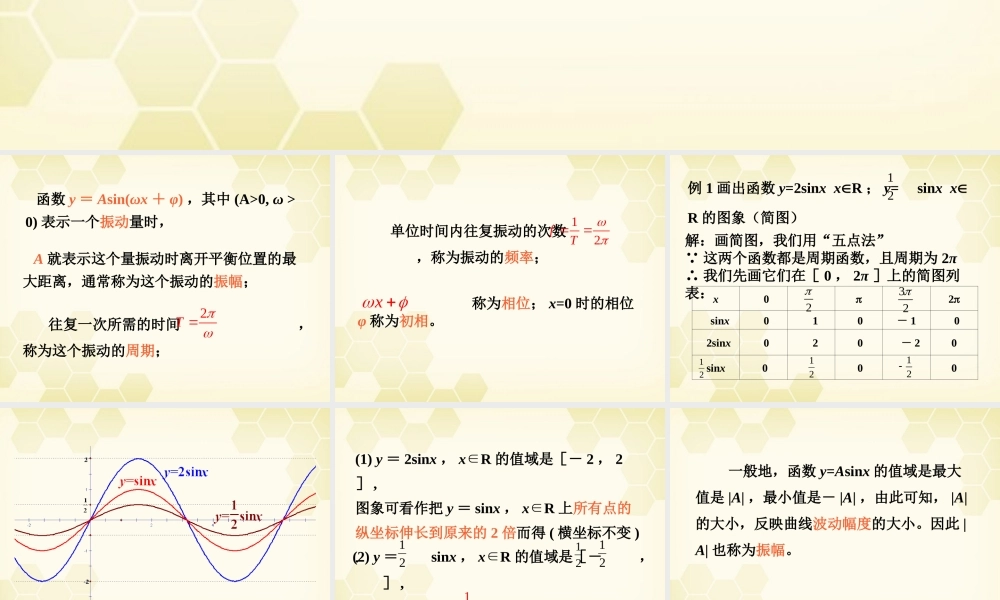
1.3.1 正弦型函数 y=Asin(ωx+φ) 的图象 函数 y ＝ Asin(ωx ＋ φ) ，其中 (A>0, ω >0) 表示一个振动量时， A 就表示这个量振动时离开平衡位置的最大距离，通常称为这个振动的振幅； 往复一次所需的时间 ，称为这个振动的周期； 2T 单位时间内往复振动的次数 ，称为振动的频率； 12fT 称为相位； x=0 时的相位φ 称为初相。x 例 1 画出函数 y=2sinx xR ； y= sinx xR 的图象（简图）21解：画简图，我们用“五点法” 这两个函数都是周期函数，且周期为 2π∴ 我们先画它们在［ 0 ， 2π ］上的简图列表： -x 02 sinx 0 1 0－ 1 0 2sinx 0 2 0 － 20sinx 0 00212112232 (1) y ＝ 2sinx ， xR∈的值域是［－ 2 ， 2］ ,图象可看作把 y ＝ sinx ， xR∈上所有点的纵坐标伸长到原来的 2 倍而得 ( 横坐标不变 ) .(2) y ＝ sinx ， xR∈的值域是［－ ， ］ ,图象可看作把 y ＝ sinx ， xR∈上所有点的纵坐标缩短到原来的 倍而得 ( 横坐标不变 ).21212112 一般地，函数 y=Asinx 的值域是最大值是 |A| ，最小值是－ |A| ，由此可知， |A|的大小，反映曲线波动幅度的大小。因此 |A| 也称为振幅。 1 ． y=Asinx ， xR(A>0 且 A1) 的图象可以看作把正弦曲线上的所有点的纵坐标伸长(A>1) 或缩短 (0