高中数学 第3讲 逆矩阵与逆变换的解题技巧素材 新人教A版选修4 2 素材VIP免费

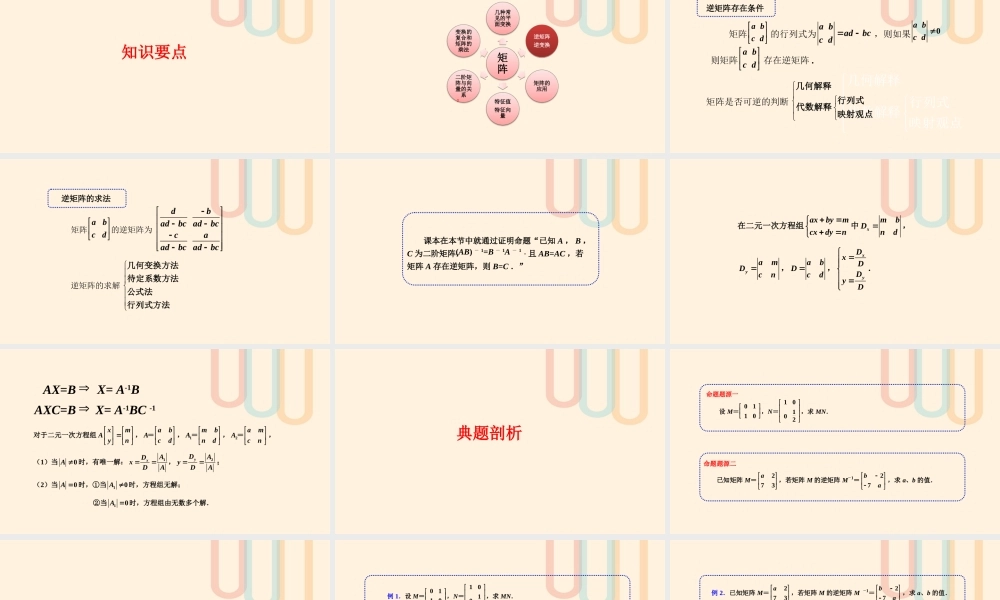
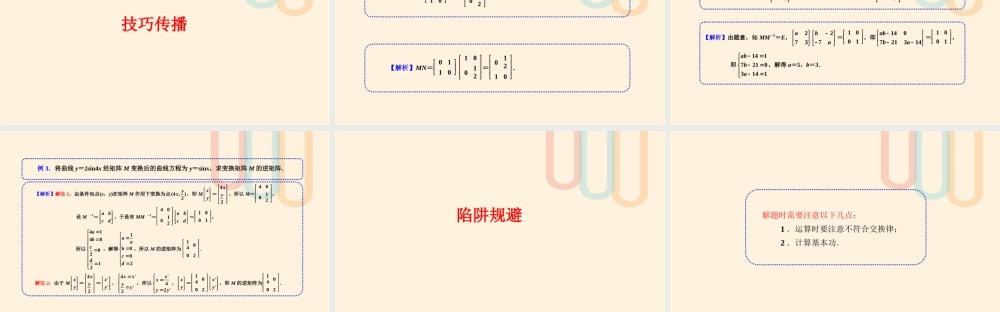
逆矩阵与逆变换解题技巧知识要点矩阵几种常见的平面变换逆矩阵逆变换逆矩阵逆变换矩阵的应用特征值特征向量二阶矩阵与向量的关系变换的复合和矩阵的乘法2逆矩阵存在条件 矩阵的行列式为，则如果 则矩阵存在逆矩阵 . a bc d a badbcc d  0 a bc d  a bc d矩阵是否可逆的判断几何解释行列式代数解释映射观点几何解释行列式代数解释映射观点 dbadbc adbccaadbc adbc矩阵的逆矩阵为 abcd逆矩阵的求解几何变换方法待定系数方法公式法行列式方法逆矩阵的求法 课本在本节中就通过证明命题“已知 A ， B ，C 为二阶矩阵， 且 AB=AC ，若矩阵 A 存在逆矩阵，则 B=C ．”(AB) － 1=B － 1A － 1 ． 在二元一次方程组 axbymcxdyn中xmbDnd ， yamDcn ，abDcd ，xyDxDDyD． AX=B  X= A-1B AXC=B  X= A-1BC -1 对于二元一次方程组xmA yn，abAcd ＝ ，1mbAnd ＝ ，2amAcn ＝ ， （1）当0A  时，有唯一解：1xADxDA，2yDAyDA； （2）当0A  时，①当10A  时，方程组无解； ②当10A  时，方程组由无数多个解． 典题剖析命题题源一 设 M＝0110，N＝10012，求 MN． 命题题源二 已知矩阵 M＝273a ，若矩阵 M 的逆矩阵 M－1＝27ba ，求 a、b 的值． 技巧传播例 1．设 M＝0110，N＝10012，求 MN． 【解析】MN＝0110 10012＝01210． 【解析】由题意，知 MM－1＝E，273a 27ba ＝1001，即140721314abba ＝1001， 即14172103141abba，解得 a＝5，b＝3． 例 2．已知矩阵 M＝273a ，若矩阵 M 的逆矩阵 M －1＝27ba ，求 a、b 的值． 例 3．将曲线 y＝2sin4x 经矩阵 M 变换后的曲线方程为 y＝sinx，求变换矩阵 M 的逆矩阵． 【解析】解法 1：由条件知点(x，y)在矩阵 M 作用下变换为点(4 ,)2yx，即 M xy...