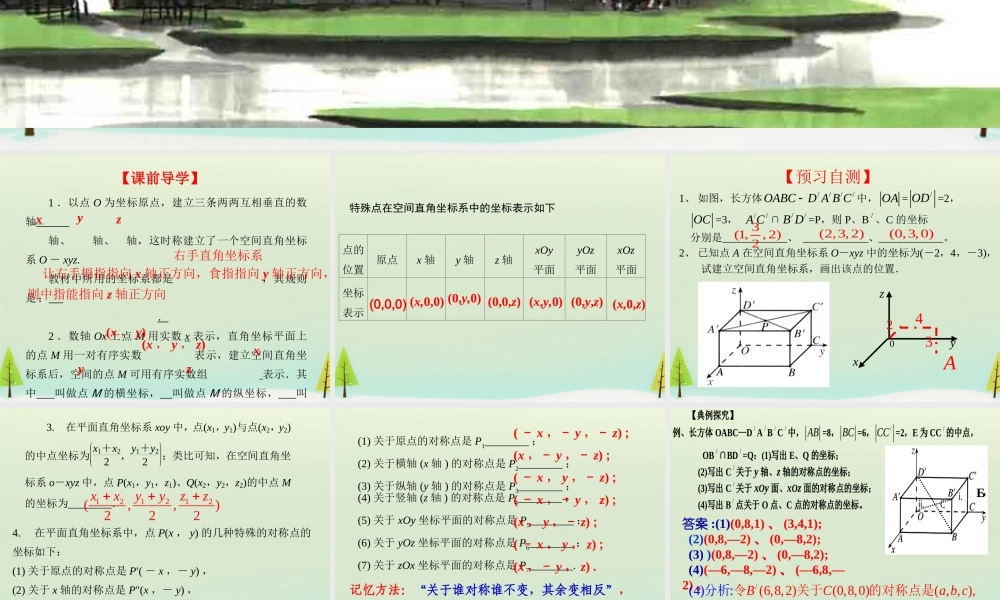
4.3.1 空间直角坐标系1 .以点 O 为坐标原点,建立三条两两互相垂直的数轴 轴、轴、轴,这时称建立了一个空间直角坐标系 O - xyz.教材中所用的坐标系都是,其规则是: .2 .数轴 Ox 上点 M 用实数 x 表示,直角坐标平面上的点 M 用一对有序实数表示,建立空间直角坐标系后,空间的点 M 可用有序实数组 表示.其中 叫做点 M 的横坐标, 叫做点 M 的纵坐标, 叫做点 M 的竖坐标.右手直角坐标系让右手拇指指向 x 轴正方向,食指指向 y 轴正方向,则中指能指向 z 轴正方向(x , y)(x , y , z)xyz 【课前导学】xyz特殊点在空间直角坐标系中的坐标表示如下 点的位置原点x 轴y 轴z 轴xOy平面yOz平面xOz平面坐标表示 (0,0,0) (x,0,0) (0,y,0) (0,0,z) (x,y,0) (0,y,z) (x,0,z)【预习自测】1、 如图,长方体////OABCD A B C中, OA =/OD =2, OC =3, //A C ∩//B D =P,则 P、B / 、C 的坐标 分别是____________、 ____________、____________。 2、 已知点 A 在空间直角坐标系 O-xyz 中的坐标为(-2,4,-3), 试建立空间直角坐标系,画出该点的位置. z 0 y x 3(1,,2)2(2,3,2)(0,3,0)A4233. 在平面直角坐标系 xoy 中,点(x1,y1)与点(x2,y2)的中点坐标为x1+x22,y1+y22;类比可知,在空间直角坐标系 o-xyz 中,点 P(x1,y1,z1)、Q(x2,y2,z2)的中点 M的坐标为________. 4. 在平面直角坐标系中,点 P(x , y) 的几种特殊的对称点的坐标如下:(1) 关于原点的对称点是 P′( - x ,- y) ,(2) 关于 x 轴的对称点是 P″(x ,- y) ,(3) 关于 y 轴的对称点是 P ( - x , y) ,那么,在空间直角坐标系内,点 P(x , y , z) 的几种特殊的对称点坐标:121212(,,)222xxyyzz(1) 关于原点的对称点是 P1________ ;(2) 关于横轴 (x 轴 ) 的对称点是 P2________ ;(3) 关于纵轴 (y 轴 ) 的对称点是 P3________ ;(4) 关于竖轴 (z 轴 ) 的对称点是 P4________ ;(5) 关于 xOy 坐标平面的对称点是 P5________ ;(6) 关于 yOz 坐标平面的对称点是 P6________ ;(7) 关于 zOx 坐标平面的对称点是 P7________.( - x ,- y ,- z) ;(x ,- y ,- z) ;( - x , y ,- z) ;( - x ,- y , z) ;(x , y ,...