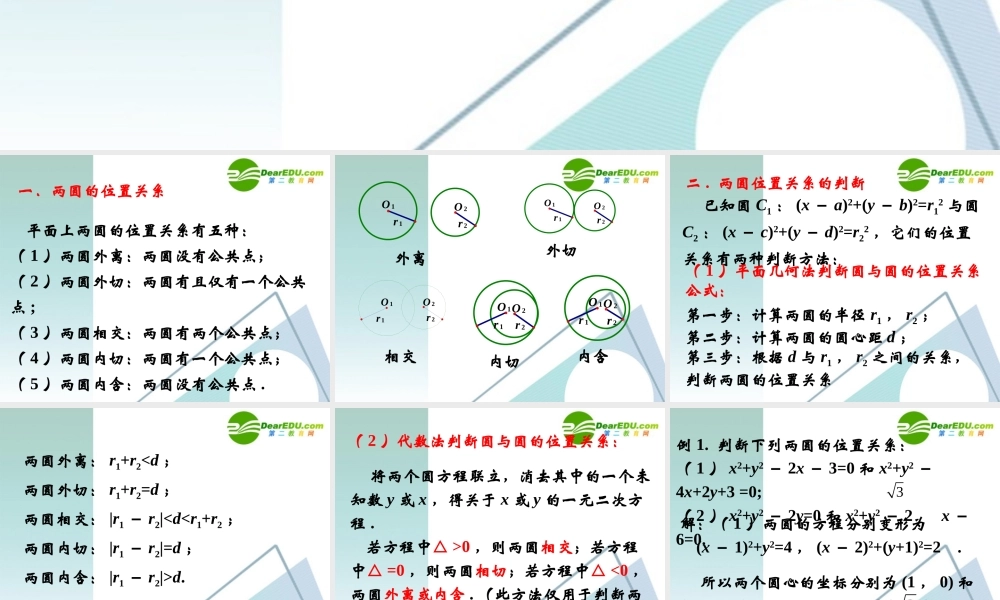
2.3.4 圆与圆的位置关系一.两圆的位置关系 平面上两圆的位置关系有五种:( 1 )两圆外离:两圆没有公共点;( 2 )两圆外切:两圆有且仅有一个公共点 ;( 3 )两圆相交:两圆有两个公共点;( 4 )两圆内切:两圆有一个公共点;( 5 )两圆内含:两圆没有公共点 .r 2r 1O 2O 1r 2r 1O 2O 1r 2r 1O 2O 1r 2r 1O 2O 1r 2r 1O 2O 1外离外切相交内切内含二 . 两圆位置关系的判断 已知圆 C1 : (x - a)2+(y - b)2=r12 与圆C2 : (x - c)2+(y - d)2=r22 ,它们的位置关系有两种判断方法:( 1 )平面几何法判断圆与圆的位置关系公式: 第一步:计算两圆的半径 r1 , r2 ;第二步:计算两圆的圆心距 d ;第三步:根据 d 与 r1 , r2 之间的关系,判断两圆的位置关系 两圆外离: r1+r2d.( 2 )代数法判断圆与圆的位置关系: 将两个圆方程联立,消去其中的一个未知数 y 或 x ,得关于 x 或 y 的一元二次方程 . 若方程中△ >0 ,则两圆相交;若方程中△ =0 ,则两圆相切;若方程中△ <0 ,两圆外离或内含 . (此方法仅用于判断两个圆的位置关系,不适用于其他的二次曲线的位置关系的判断问题)解:( 1 )两圆的方程分别变形为 (x - 1)2+y2=4 , (x - 2)2+(y+1)2=2 . 所以两个圆心的坐标分别为 (1 , 0) 和(2 ,- 1) ,两圆的圆心距 d=|C1C2|= ,2例 1. 判断下列两圆的位置关系:( 1 ) x2+y2 - 2x - 3=0 和 x2+y2 -4x+2y+3 =0;( 2 ) x2+y2 - 2y=0 和 x2+y2 - 2 x -6=0.3由 |r1 - r2|=2 - , r1+r2=2+ ,因为 2 - < <2+ ,所以这两个圆相交。22222( 2 ) x2+y2 - 2y=0 和 x2+y2 - 2 x -6=0.3( 2 )两圆的方程分别变形为 x2+(y - 1)2=12 , (x - )2+y2=32.3所以两圆内切。由 |r1 - r2|=2 , 所以两个圆心的坐标分别为 (0 , 1) 和( , 0) ,3 两圆的圆心距 d=|C1C2|=2 ,例 2 .已知圆 C1 : x2+y2 - 10x - 10y=0和圆 C2 : x2+y2+6x+2y - 40=0 相交于A 、 B 两点,求公共弦 AB 的长 .解法一:由两圆的方程相减,消去二次项得到一个二元一次方程,此方程即为公共弦 AB 所在的...