高中数学任意角的三角函数 课件 新人教A版必修4 课件VIP免费

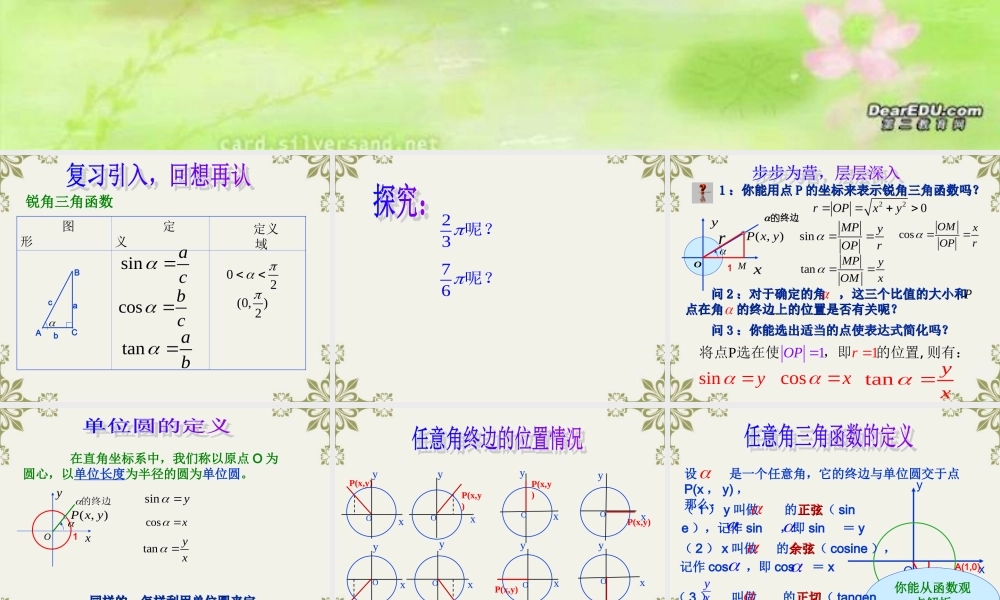
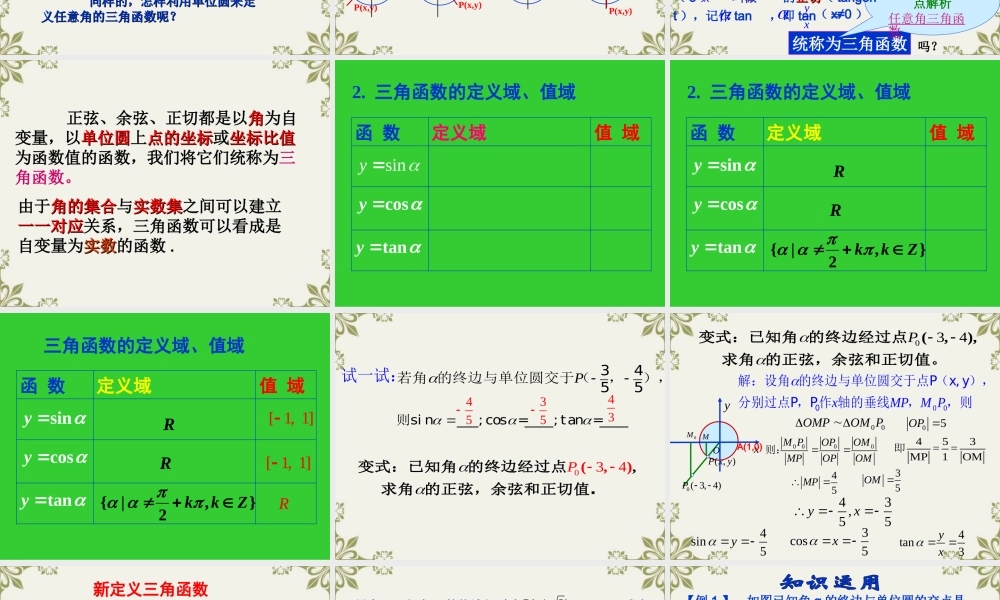
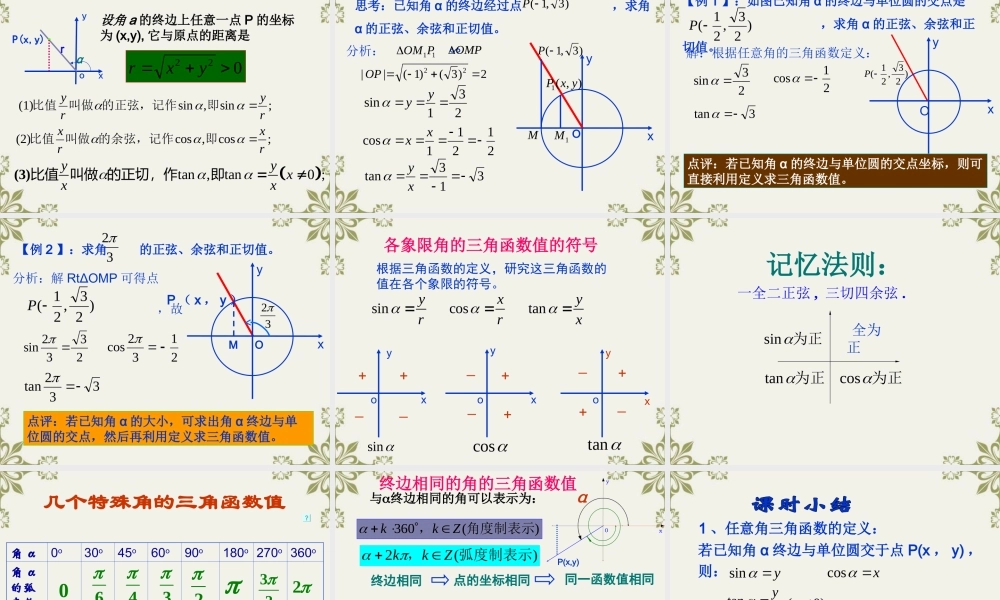
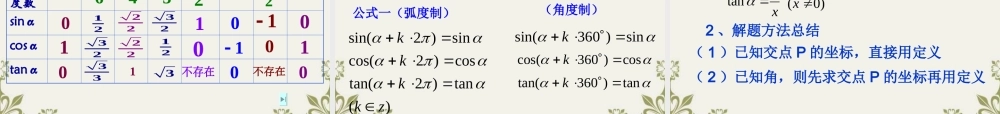锐角三角函数 图 形 定 义tanab cosbc sinac (0,)2 定义域CABbca02 23呢？76呢？ 终边的( , )P x yyxO 11 ：你能用点：你能用点 PP 的坐标来表示锐角三角函数吗？的坐标来表示锐角三角函数吗？MsinMPyOPr r220rOPxytanMPyOMx cosOMxOPr  问 问 22 ：对于确定的角 ，这三个比值的大小和 ：对于确定的角 ，这三个比值的大小和 点在角 的终边上的位置是否有关呢？点在角 的终边上的位置是否有关呢？ P 问问 33 ：你能选出适当的点使表达式简化吗？：你能选出适当的点使表达式简化吗？11POPr将点 选在使，即的位置, 则有：siny cosx tanyx 1 在直角坐标系中，我们称以原点 O 为圆心，以单位长度为半径的圆为单位圆。 同样的，怎样利用单位圆来定同样的，怎样利用单位圆来定义任意角的三角函数呢？义任意角的三角函数呢？siny cosx tanyx y的终边xO( , )P x y1 P(x,y)P(x,y)P(x,y)P(x,y)OyxOyxOyxyxO·P(x,y)P(x,y)P(x,y)P(x,y)·yxOyxOyxOyxO OxP(x ， y)统称为三角函数你能从函数观点解析任意角三角函数吗？ 设 是一个任意角，它的终边与单位圆交于点P(x ， y) ，那么：（ 2 ） x 叫做 的余弦余弦（ cosine ），记作 cos ，即 cos ＝ x（ 1 ） y 叫做 的正弦正弦（ sine ），记作 sin ，即 sin ＝ y（ 3 ） 叫做 的正切正切（ tangent ），记作 tan ，即 tan ＝yxyxA(1,0)y（ x≠0 ） 正弦、余弦、正切都是以角角为自变量，以单位圆单位圆上点的坐标点的坐标或坐标比值坐标比值为函数值的函数，我们将它们统称为三角函数。由于角的集合角的集合与实数集实数集之间可以建立一一对应一一对应关系，三角函数可以看成是自变量为实数实数的函数 . 2. 三角函数的定义域、值域函 数定义域值 域 2. 三角函数的定义域、值域函 数定义域值 域RR},2|{Zkk 三角函数的定义域、值域函 数定义域值 域RR},2|{ZkkR[ 1, 1][ 1, 1] 试一试：则si n___; cos =____; tan =____4535P34若角 的终边与单位圆交于（-，-），5543034P(,),变式：已知角 的终边经过点求角 的正弦，余弦和正切值. 034P(,),变式：已知角 的终边经过点求角 的正弦，余弦和正切...