浙江省金华市高一数学 221对数与对数运算(第二课时)课件VIP免费

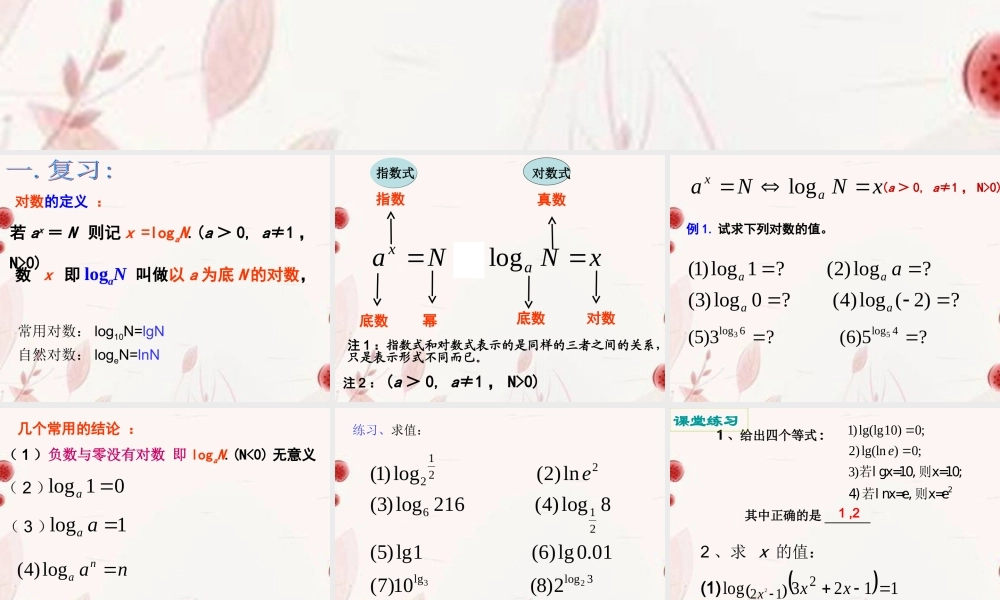
2.2.1 对数与对数运算 若 ax ＝ N 则记 x =logaN.(a ＞ 0, a≠1 ，N>0)对数的定义 ：数 x 即 logaN 叫做以 a 为底 N 的对数，常用对数： log10N=lgN自然对数： logeN=lnNxNNaaxlog指数真数底数对数幂底数指数式对数式注 1 ：指数式和对数式表示的是同样的三者之间的关系，只是表示形式不同而已。注 2 ： (a ＞ 0, a≠1 ， N>0)例 1. 试求下列对数的值。?)2(log)4(?0log)3(?log)2(?1log)1(aaaaa?5)6(?3)5(4log6log53xNNaaxlog(a ＞ 0, a≠1 ， N>0)（ 1 ）负数与零没有对数 即 logaN.(N<0) 无意义（ 2 ）01loga（ 3 ）1logaa几个常用的结论 ：loga NaN（ 5 ）nanalog)4(练习、求值：3loglg2162212232)8(10)7(01.0lg)6(1lg)5(8log)4(216log)3(ln)2(log)1(e1 、给出四个等式 :1)lg(lg10)0;2)lg(ln )0;3)e2若l gx=10, 则x=10;4)若l nx=e, 则x=e其中正确的是 ________1 ,22 、求 x 的值： (1) 1123log2122xxx(2)0logloglog432x课堂练习思考 1: 求下列三个对数的值： log232 ， log24 ， log28 ．你能发现这三个对数之间有哪些内在联系？思考 2: 将 log232 － log24=log28 推广到一般情形有什么结论？怎样证明？ 思考 3:log23 与 log281 有什么关系？R)M(nnMNMNMNMN)(Manaaaaaaaloglog3logloglog2logloglog1）（）（）（如果 a > 0 ， a  1 ， M > 0 ， N > 0 有：对数的运算对数的运算例 1 用 logax ， logay ， logaz 表示下列各式：(1) ; (2) . loga xyz23logaxyz例 2 求下列各式的值： (1) log2 （ 47×25 ）； (2) log318 -log32 (3) (4) 8log3136.0log2110log3log2log2555552log123350lg2lg)5(lg(4)2log 32－log 3329 ＋log 38－5 log53； (5)lg 27＋lg8－lg 1000lg1.2. 练习： (1)4lg2＋3lg5－lg15； (2)1＋12lg9－lg2401－23lg27＋lg365； (3)lg37＋lg70－lg3； (4)lg22＋lg5·lg20－1.