高中数学 432空间两点间的距离公式课件 新人教A版必修2 课件VIP免费

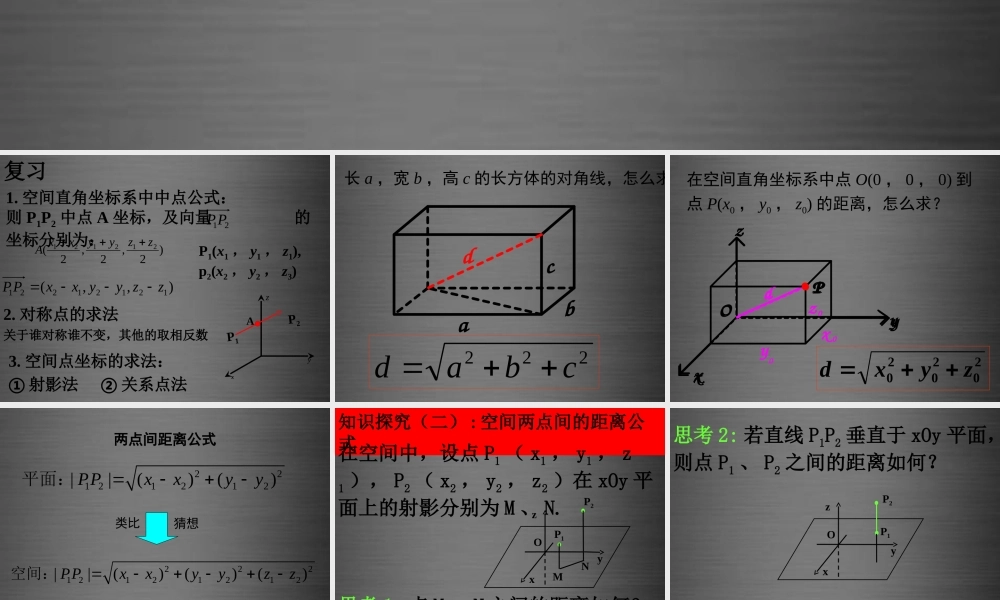
复习2. 对称点的求法3. 空间点坐标的求法：① 射影法② 关系点法)2,2,2(212121zzyyxxA),,(12121221zzyyxxPP1. 空间直角坐标系中中点公式：则 P1P2 中点 A 坐标，及向量 的坐标分别为：21PPxyzP2P1AP1(x1 ， y1 ， z1),p2(x2 ， y2 ， z3)关于谁对称谁不变，其他的取相反数长 a ，宽 b ，高 c 的长方体的对角线，怎么求？222cbadcbad在空间直角坐标系中点 O(0 ， 0 ， 0) 到点 P(x0 ， y0 ， z0) 的距离，怎么求？202020zyxdOPzyxdOPzyxdx 0y0z 0两点间距离公式22121212||()()PPxxyy平面：类比猜想22212121212||()()()PPxxyyzz空间：知识探究（二） : 空间两点间的距离公式 在空间中，设点 P1 （ x1 ， y1 ， z1 ）， P2 （ x2 ， y2 ， z2 ）在 xOy 平面上的射影分别为 M 、 N.xyzOP2MP1N思考 1: 点 M 、 N 之间的距离如何？221221yyxxMN思考 2: 若直线 P1P2 垂直于 xOy 平面，则点 P1 、 P2 之间的距离如何？xyzOP2P12121zz PP思考 3: 若直线 P1P2 平行于 xOy 平面，则点 P1 、 P2 之间的距离如何？MNxyzOP2P122122121yyxxMNPP思考 4: 若直线 P1P2 是 xOy 平面的一条斜线，则点 P1 、 P2 的距离如何计算？MNxyzOP2P1A22122122121zz yyxxPP思考与探究 2 ：如果 P1(x1 ， y1 ， z1),P2(x2 ， y2 ， z3),|P1P2| 如何计算？xyzP2),,(12121221zzyyxxPP即：22122122121||zzyyxxPP结论 2P1方法一：射影法 方法二：向量法在空间直角坐标系中，点 P(x1,y1,z1) 和点 Q(x2,y2,z2) 的中点坐标 (x,y,z):121212222xxxyyyzzz二、空间中点坐标公式：例 1 求证以)1,3,4(1M、)2,1,7(2M、)3,2,5(3M 三点为顶点的三角形是一个等腰三角形. 解221MM,14)12()31()47(222232MM,6)23()12()75(222213MM,6)31()23()54(22232MM,13MM原结论成立 .练 1: 已知三角形的三个顶点 A(1,5,2) ，B(2,3,4) ， C(3,1,5) ，求 :(1) 三角形三边的边长；解 :3423521222AB6541332222BC29521531222AC练 1: 已知三角形的三个顶点 A(1...