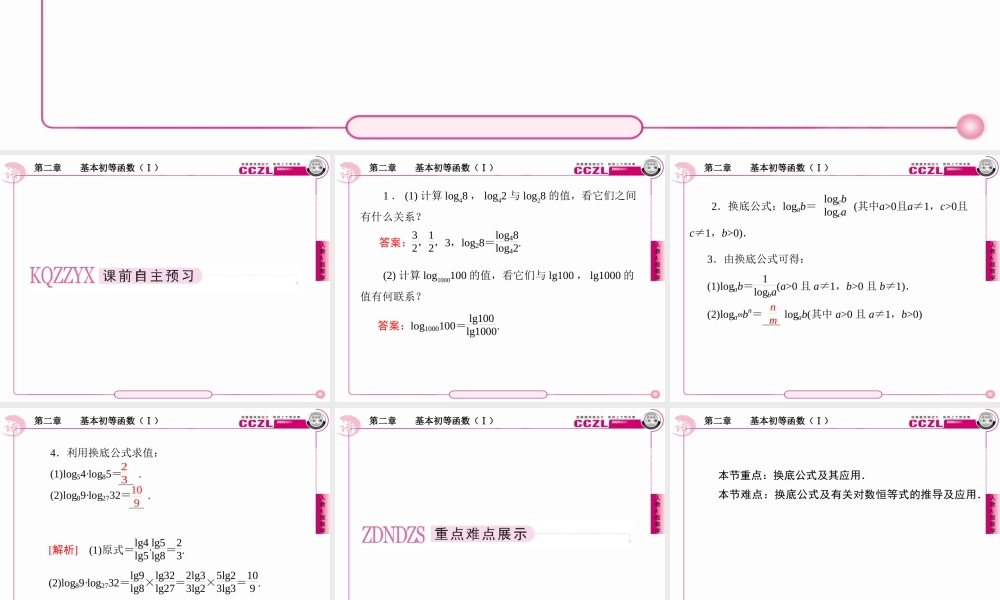
第二章 基本初等函数(Ⅰ)人教A版数学第二章 基本初等函数(Ⅰ)人教A版数学第二章 基本初等函数(Ⅰ)人教A版数学1 . (1) 计算 log48 , log42 与 log28 的值,看它们之间有什么关系?(2) 计算 log1000100 的值,看它们与 lg100 , lg1000 的值有何联系?答案:32,12,3,log28=log48log42. 答案:log1000100= lg100lg1000. 第二章 基本初等函数(Ⅰ)人教A版数学2.换底公式:logab= logcblogca (其中a>0且a≠1,c>0且c≠1,b>0). 3.由换底公式可得: (1)logab= 1logba(a>0 且 a≠1,b>0 且 b≠1). (2)logambn= logab(其中 a>0 且 a≠1,b>0) nm 第二章 基本初等函数(Ⅰ)人教A版数学4.利用换底公式求值: (1)log54·log85= . (2)log89·log2732= . [解析] (1)原式=lg4lg5·lg5lg8=23. (2)log89·log2732=lg9lg8×lg32lg27=2lg33lg2×5lg23lg3=109 . 109 23 第二章 基本初等函数(Ⅰ)人教A版数学第二章 基本初等函数(Ⅰ)人教A版数学本节重点:换底公式及其应用.本节难点:换底公式及有关对数恒等式的推导及应用.第二章 基本初等函数(Ⅰ)人教A版数学第二章 基本初等函数(Ⅰ)人教A版数学换底公式:logab=logcblogca的证明如下: 令logab=x,则b=ax.两边同取以 c为底的对数得logcb=logcax=xlogca,所以 x=logcblogca,即 logab=logcblogca. 它还可以用对数恒等式来证明:要证 logab=logcblogca,即证 logab·logca=logcb.由对数的运算法则,即证 logcalogab=logcb, alogab=b,∴上式成立,∴原结论成立. 第二章 基本初等函数(Ⅰ)人教A版数学第二章 基本初等函数(Ⅰ)人教A版数学[例1] 计算log2125·log318·log519. [分析] 将底统一成以10为底的常用对数 [解析] 原式=lg 125lg2 ·lg18lg3·lg19lg5 =(-2lg5)·(-3lg2)·(-2lg3)lg2lg3lg5=-12. 第二章 基本初等函数(Ⅰ)人教A版数学(1)求证:loganbn=logab.(a>0 且 a≠1,n∈N+,b>0). (2)求证:logambn=nmlogab(a<0 且 a≠1,b>0) [解析] (1)loganbn=logabnlogaan=nlogabnlogaa=logab; (2)logambn=logabnlogaam=nlogabmlogaa=nmlogab. 第二章 基本初等函数(Ⅰ)人教A版数学第二章 基本初等函数(Ⅰ)人教A版数学[ 例 2] 某城市现有人口总数为 100 万,如果年自然增长率为 1.2% ,试解答下面的问题:(1) 写出该城市人口总数 y(...