高二数学 第八章 圆锥曲线方程： 8.4双曲线的简单几何性质优秀课件VIP免费

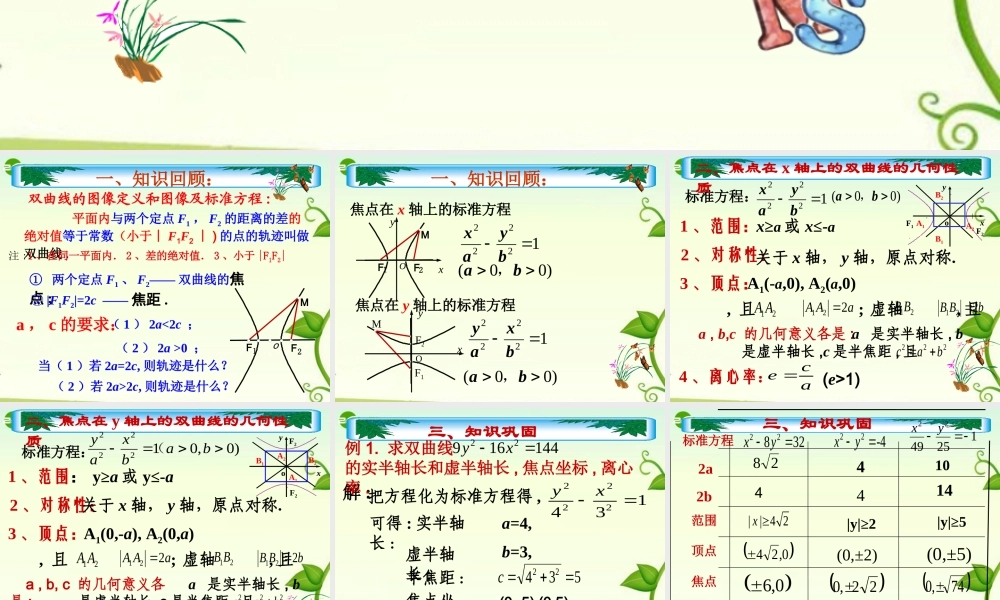
一、知识回顾：① 两个定点 F1 、 F2—— 双曲线的焦点 ; ② |F1F2|=2c —— 焦距 .（ 1 ） 2a<2c ；oF2F1M 平面内与两个定点 F1 ， F2 的距离的差的绝对值等于常数（小于︱ F1F2 ︱ ) 的点的轨迹叫做双曲线 .（ 2 ） 2a >0 ；当（ 1 ）若 2a=2c, 则轨迹是什么？（ 2 ）若 2a>2c, 则轨迹是什么？a ， c 的要求：注 :1 、在同一平面内． 2 、差的绝对值． 3 、小于 |F1F2|双曲线的图像定义和图像及标准方程 :一、知识回顾：12222 byax12222 bxay焦点在 y 轴上的标准方程OMF2F1xy)00(ba，F2F1MxOy)00(ba，焦点在 x 轴上的标准方程标准方程：ace 1 、范围：x≥a 或 x≤-a2 、对称性：关于 x 轴， y 轴，原点对称．3 、顶点：A1(-a,0), A2(a,0)实轴 , 且 ; 虚轴 , 且 .4 、离心率：(e>1) a , b,c 的几何意义各是 : a 是实半轴长 , b是虚半轴长 ,c 是半焦距 , 且222bacaAA221bBB22121BB21AA12222 byax)00(ba，yoxB1B2A1A2F1F2二、焦点在 x 轴上的双曲线的几何性质实轴 , 且 ; 虚轴 , 且 .二、焦点在 y 轴上的双曲线的几何性质标准方程：ace )0,012222babxay（1 、范围： y≥a 或 y≤-a2 、对称性：关于 x 轴， y 轴，原点对称．3 、顶点：A1(0,-a), A2(0,a)oyxB1B2A1A2F2F25 、离心率：(e>1) a , b, c 的几何意义各是 : a 是实半轴长 , b是虚半轴长 ,c 是半焦距 , 且222bacaAA221bBB22121BB21AA三、知识巩固把方程化为标准方程得 ,1342222 xy可得 : 实半轴长 :53422c虚半轴长 :半焦距 :焦点坐标 :离心率 :45ace解 :a=4,b=3,例 1. 求双曲线 的实半轴长和虚半轴长 , 焦点坐标 , 离心率 .14416922xy(0,-5),(0,5),三、知识巩固离心率焦点顶点范围 2a标准方程32822 yx-422 yx1254922 yx28| | 4 2x 0,240,6423e44|y|≥2(0,±2)22,0 2e1014|y|≥5(0,±5)74,0 574e42b三、知识巩固例 2. 已知双曲线的中心在原点，对称轴为坐 标轴 , 它的一个焦点 , 且离心率 e 可 以使方程 有相等的实 根，求满足条件的双曲线方程．)0,5(F041)1(22xex三、知识巩固例 3. 已知双曲线虚轴的一个端点为 M, 两焦点分别 , , 且 , 则双曲线的离心率 为 ( ) 2F1F...