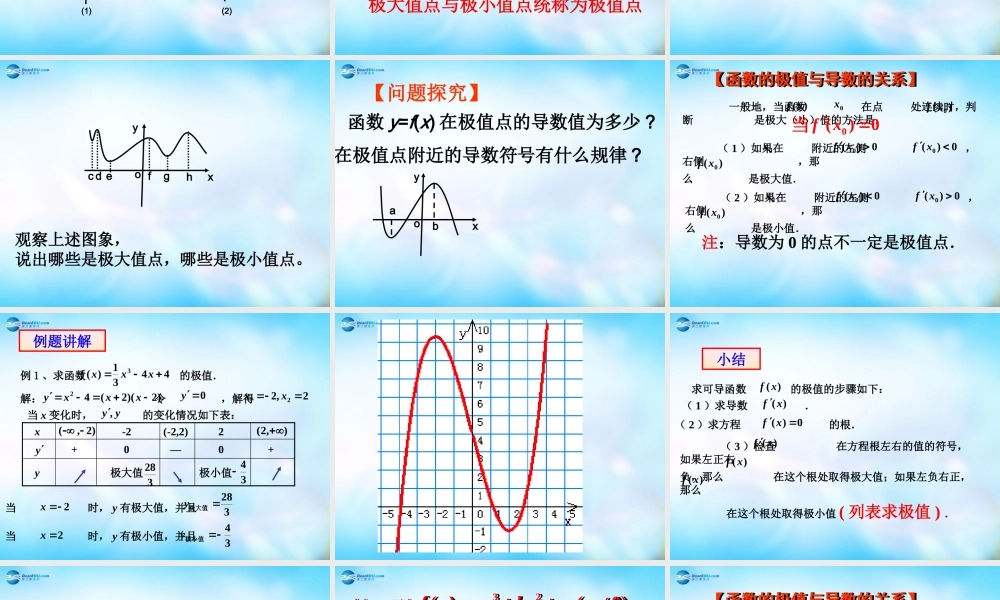
1.3.2 函数的极值与导数一般地,函数的单调性与其导函数的正负有如下关系:在某个区间 内,如果)(xfy 0)( xf,那么0)( xf()ab,函数 在这个区间内单调递增;如果,那么函数 在这个区间内单调递减。)(xfy 知识回顾(2) 求导数).(xf (3) 解不等式 ; 或解不等式 .¢f (x) < 0¢f (x) > 0= ( )yf x(1) 求 的定义域 D(4) 与定义域求交集利用导数讨论函数单调性的一般步骤 :(5) 写出单调区间htoab观察:如下图,我们发现,当 t=a 时,高台跳水运动员距离水面的高度最大,那么函数 h(t) 在此点的导数是多少呢?此点附近的图像有什么特点?相应的导数的符号有什么变化规律?思考:思考:对于一般的函数 y=f(x) 是否也有类似的性质呢?如下图 (1)(2) 函数 y=f(x) 在 a,b,c,d,e,f,g,h 等点的函数值与这些点附近的函数值有什么关系? y=f(x) 在这些点附近的导数值是多少?在这些点附近, y=f(x) 的导数符号有什么变化规律?yxoabyxoc d efgh(1)(2)【函数极值的定义】 设函数 y=f(x) 在 x=x0 及其附近有定义,(1) 如果在 x=x0 处的函数值比它附近所有各点的 函数值都大,即 f(x)f(x0) ,则称 f(x0) 是函数 y=f(x)的一个极小值。记作 :y 极小值 =f(x0) ,点 x0 为极大值点。极大值与极小值统称为极值极大值点与极小值点统称为极值点【关于极值概念的几点说明】(1) 极值反映了函数在某一点附近的大小情况,刻画的是函数的局部性质;(2) 极值点是自变量的值,极值指的是函数值 ;(3) 函数的极大 ( 小 ) 值可能不止一个 ,而且函数的极大值未必大于极小值 ;(4) 函数的极大 ( 小 ) 值只能在定义域内部取得,不能在定义区间的端点取得 ;观察上述图象,说出哪些是极大值点,哪些是极小值点。yxoc d efgh【问题探究】 函数 y=f(x) 在极值点的导数值为多少 ?在极值点附近的导数符号有什么规律 ?yxoab 一般地,当函数 在点 处连续时,判断 是极大(小)值的方法是:0x)(xf)(0xf ( 1 )如果在 附近的左侧 ,右侧 ,那么 是极大值.0x0)(0 xf0)(0 xf)(0xf ( 2 )如果在 附近的左侧 ,右侧 ,那么 是极小值.0x0)(0 xf0)(0 xf)(0xf...