高中数学 平面向量基本定理课件 新人教B版必修4 课件VIP免费

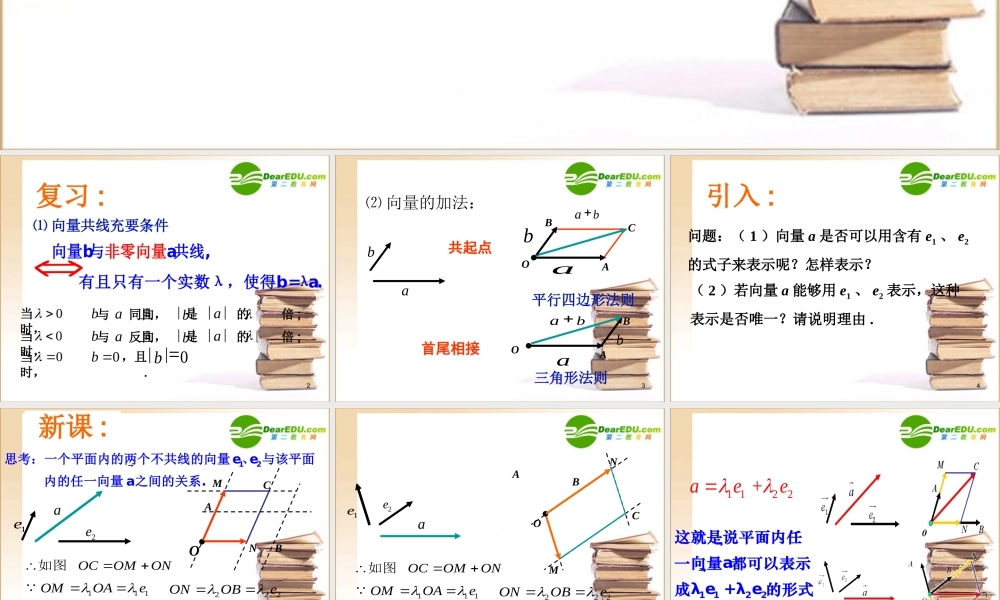
平面向量基本定理 2非零向 向量 与量ba共线,当 时， 0 与 同向，ba且 是 的 倍 ;||b||a当 时， 0 与 反向，ba且 是 的 倍 ;||b||a||当 时， 0 0b ，且 .|| 0b 有且只有一个实数λ，使得b=λa.⑴ 向量共线充要条件复习 :3ab⑵ 向量的加法：OBCAabOAaBbba ba 平行四边形法则三角形法则共起点首尾相接4问题：（ 1 ）向量 a 是否可以用含有 e1 、 e2的式子来表示呢？怎样表示？（ 2 ）若向量 a 能够用 e1 、 e2 表示，这种表示是否唯一？请说明理由 .引入 :51e�2e�OCABMN OCOMON�如图11 1OMOAe�1 122OCee�1 122 +aee��即222ONOBe�a�12思考：一个平面内的两个不共线的向量 e、e 与该平面 内的任一向量 a之间的关系.新课 :61e�2e�OCABMNa OCOMON�如图11 1OMOAe�1 122OCee�1 122 +aee��即222ONOBe�71 122 +aee����1122这就是说平面内任一向量a都可以表示成λ e +λ e 的形式8平面向量基本定理 如果 e1 、 e2 是平面内的两个不共线向量，那么对于这一平面内的任一向量 a ，有且只有一对实数 a1 、 a2 ，使 1 122aaaee说明：① e1 、 e2 是两个不共线的向量； ② a 是平面内的任一向量； ③ a1 ， a2 实数，唯一确定 .9 �OAOMON ∴ 存 在 实 数 a1 ， a2 使1 1OMa�e ,22ONa�e . 于 是1 122 .aaaee 设存在实数 x,y 使12xyaee ，只要证1ax 且2ay NMOe 2e 1Aa1e1+a2e2=xe1+ye2,(x － a1)e1+(y － a2)e2=0( 存在性 )( 唯一性 )10 我们把不共线向量 e1 ， e2 叫做这一平面内所有向量的一组基底，记为 {e1 ， e2} ， a1e1+a2e2 叫做向量 a 关于基底 {e1 ， e2}的分解式。11例 1. 已知平行四边形 ABCD 的两条对角线相交于 M ，设 ， ，试用基底 {a ， b} 表示ABa�ADb�,,,�MA MB MC MDbaMDCBA实例 :12例 2. 已知 A, B 是 l 上任意两点， O 是 l 外一点，求证：对直线 l 上任一点 P ，存在实数t ，使 关于基底 { } 的分解式为OP�,OA OB�(1).OPt OAtOB ...