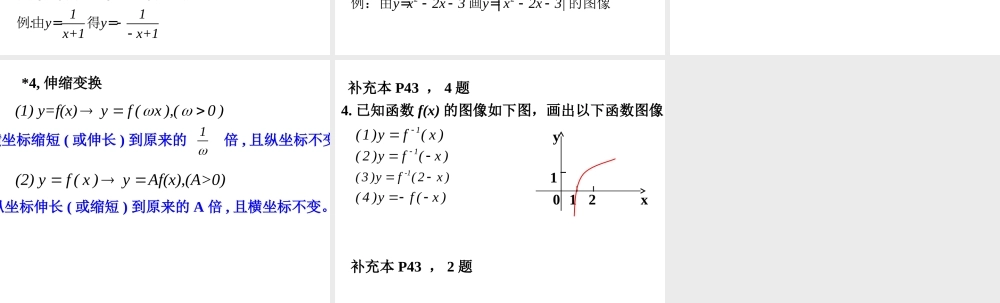
函数图象变换点的集合 {(x,y)| y=f(x),x∈A} 叫做 f(x) 的图象。什么是函数图象? 函数图象能够形象直观地刻画出变量 y 与 x的关系;定义域、值域、单调性,奇偶性等在图象上一目了然。所以,函数图象是研究函数的重要工具,掌握函数图象是学习函数的捷径。 通过分析函数的特征画函数图象:(1) 将解析式化简为熟悉的一次函数、二次函数、反比例函数等,利用这些熟悉的函数特征,可以迅速作出图象。(2) 不能将解析式化简为熟悉的函数时,那么就先分析函数的定义域、值域、与坐标轴交点、奇偶性、单调性等,从总体把握曲线的范围和变化趋势,然后列表描点作图。 函数图像变换:1 ,平移变换(1) y=f(x)yf(x+a)22y xy( x2)例, 由 = 画出的函数图像22y xy( x2)例, 由 = 画出的函数图像1yx+3练习:画出的函数图像a0,|a| 时 左移个单位a<0,|a|时 右移个单位左加右减 (2) y=f(x)yf(x)+b b0,|b| 时 上移个单位b<0,|b|时 下移个单位上加下减 1y3 x1 例:画出+ 的函数图像1y3 x1例:画出的函数图像 2 ,对称变换 (2) y=f(x)yf(x) ;将图像关于 y 轴作对称 11yyx+1x+1例,由 =得 =(1) y=f(x)yf(x) ;将图像关于 x 轴作对称 11yyx+1x+1例,由 =得 =(3) y=f(x)yf(x)作关于原点对称: 11:yyx+1x+1例由 =得 = 3, 翻折变换(1)y=f(x)y=f(|x|) ;保留 y 轴右侧,将右侧作关于 y 轴对称;(原左侧不要)22y x2x3 y x2| x| 3例:由 =画 =的图像|(2) y=f(x)yf(x)| ;保留 x 轴上方,将 x 轴下方关于 x 轴作对称 22y x2x3 yx2x3| 例:由 =画 =|的图像 1y1x1 练习:画出函数的草图1y1 |x| 1 练习:画出函数的草图 *4, 伸缩变换 (1) y=f(x)yf (x ),(0 )横坐标缩短 ( 或伸长 ) 到原来的 倍 , 且纵坐标不变 1(2) yf ( x )yAf(x),(A>0)纵坐标伸长 ( 或缩短 ) 到原来的 A 倍 , 且横坐标不变。 补充本 P43 , 2 题补充本 P43 , 4 题0 121xy4. 已知函数 f(x) 的图像如下图,画出以下函数图像1(1)yf( x )1( 2 )yf( x )-1(3 )yf ( 2x )( 4 )yf ( x )