高中数学 23平面向量基本定理及坐标运算课件 新人教A版必修4 课件VIP免费

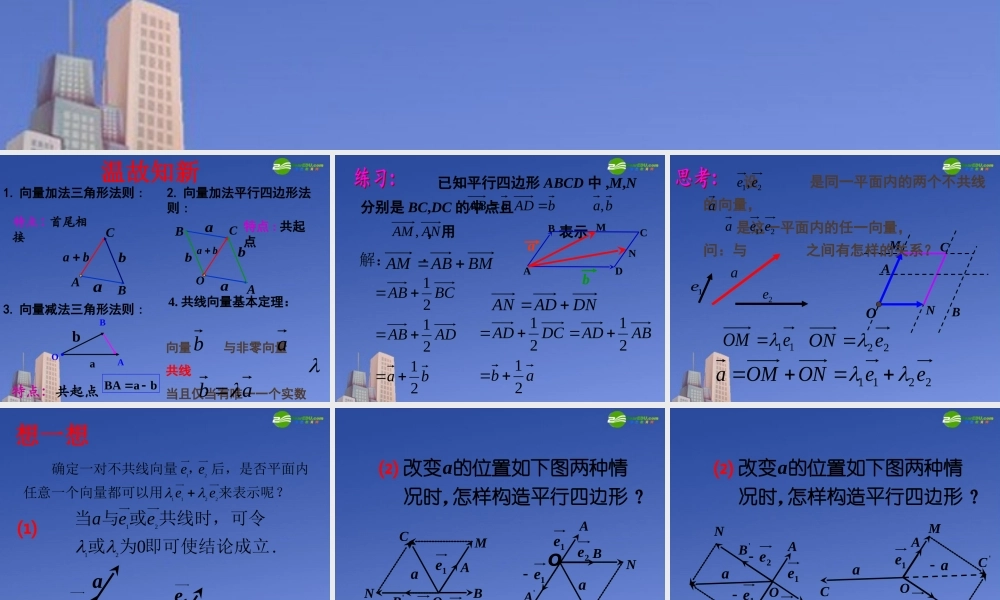
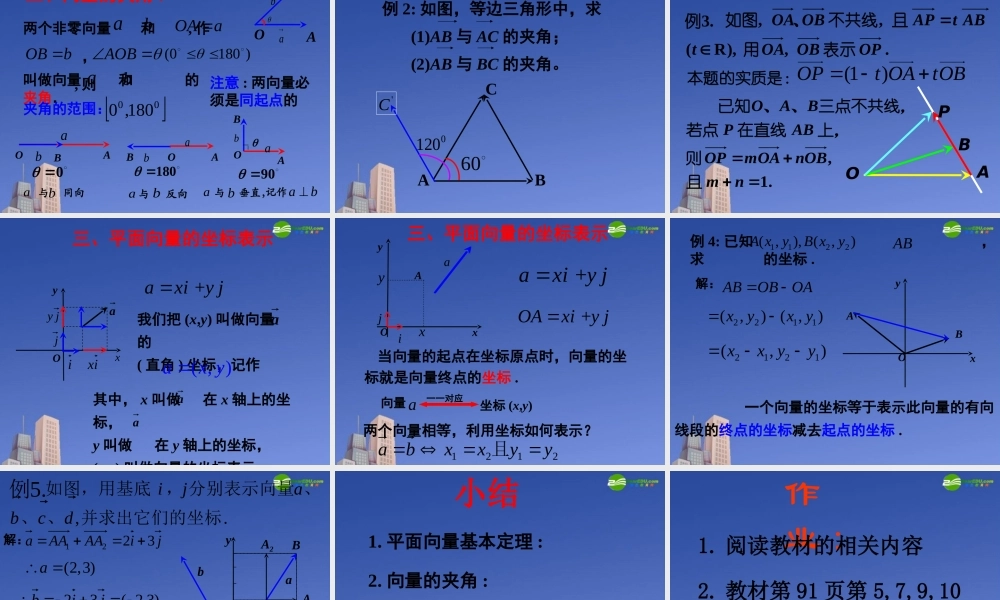
aAbBCbaaaAbBbOCba特点 : 首尾相接特点 : 共起点bBaABAab �2. 向量加法平行四边形法则 :O特点：共起点1. 向量加法三角形法则 :3. 向量减法三角形法则 :4. 共线向量基本定理： 向量 与非零向量 共线当且仅当有唯一一个实数 ，使得abab温故知新 已知平行四边形 ABCD 中 ,M,N分别是 BC,DC 的中点且 ，用 表示 . bADaAB ,ba,ANAM,ADBCMNbaBMABAM解：DNADANbaADABBCAB212121abABADDCAD2121211e�2e�OCABMNa11eOM22eON 设 是同一平面内的两个不共线的向量， 是这一平面内的任一向量，问：与 之间有怎样的关系？21,eea21,eea2211eeONOMa？来表示呢任意一个向量都可以用后，是否平面内，确定一对不共线向量 221121eeee想一想⑴a1e2ea1e2e . 02121即可使结论成立为或共线时，可令或与当eea⑵？怎样构造平行四边形况时，的位置如下图两种情改变 aa1e2ea1e2eO2eAOCB'BNMCAB'A1eNM⑵？怎样构造平行四边形况时，的位置如下图两种情改变 a1e2eaAOB'B'ANM1e2eaAOBCNM'Ca2e1e一、平面向量基本定理 :如果 是同一平面内的两个不共线向量，那么对于这一平面内的任一向量 有且只有一对实数 , 使21 ee、a21、2211eea. 21所有向量的一组基底叫做表示这一平面内，其中ee2 、基底不唯一，关键是不共线 .4 、基底给定时，分解形式唯一 .说明：1 、把不共线的非零向量 叫做表示这一平面内所有向量的一组基底 .12,e e�3 、由定理可将任一向量 在给出基底 的条件下进行分解 .12,e e�a1.练习2.3. 设 是两个不共线向量，已知 若 A,B,D 三点共线，求实数 ？ ,2bkaABkba,,3baCB,2baCDbDC21解：DCADBABCbab21ba21ANDAMDMNbab21)21(21ab 411.//2,,,,ABCDABCDABCDMNDCBAADa ABba bDC BC MN���例 如图梯形中，，，、 是，中点，，试以为基底表示aABDCNMb二、向量的夹角 :OABba两个非零向量 和 , 作 ， , 则)1800(abAOB叫做向量 和 的夹角．OAa�OBb�ab夹角的范围：00 180,0180 与 反向abOABab0 与 同向abOABab记作ab90与 垂直，abOAB ab注意 : 两向量必须是同起点...