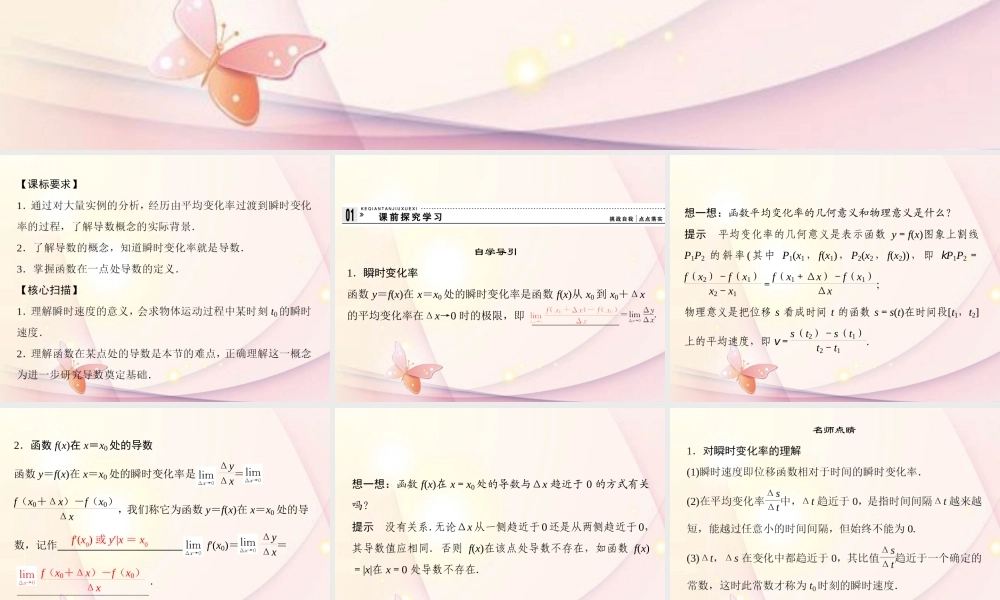
3 . 1.2 导数的概念自学导引 1.瞬时变化率 函数 y=f(x)在 x=x0 处的瞬时变化率是函数 f(x)从 x0 到 x0+Δx的平均变化率在Δx→0 时的极限,即 想一想:函数平均变化率的几何意义和物理意义是什么? 提示 平均变化率的几何意义是表示函数 y=f(x)图象上割线P1P2 的斜率(其中 P1(x1,f(x1),P2(x2,f(x2)),即 kP1P2=f(x2)-f(x1)x2-x1=f(x1+Δx)-f(x1)Δx; 物理意义是把位移 s 看成时间 t 的函数 s=s(t)在时间段[t1,t2]上的平均速度,即 v=s(t2)-s(t1)t2-t1. 2.函数 f(x)在 x=x0 处的导数 函数 y=f(x)在 x=x0 处的瞬时变化率是 lim ΔyΔx=lim f(x0+Δx)-f(x0)Δx,我们称它为函数 y=f(x)在 x=x0 处的导数,记作 ,即 f′(x0)= ΔyΔx= f(x0+Δx)-f(x0)Δx . f′(x0) 或 y′|x = x0 想一想:函数 f(x)在 x=x0 处的导数与Δx 趋近于 0 的方式有关吗? 提示 没有关系.无论Δx 从一侧趋近于 0 还是从两侧趋近于 0,其导数值应相同.否则 f(x)在该点处导数不存在,如函数 f(x)=|x|在 x=0 处导数不存在. 2.对导数概念的理解 导数是在点 x=x0 处附近ΔyΔx的极限,是一个局部概念,y=f(x)在 x=x0 处的导数 f′(x0)是一个确定的数. 注意:(1)某点导数的概念包含两层含义: ①lim ΔyΔx存在(惟一确定的值),则称函数 y=f(x)在 x=x0 处可导, ②若 lim ΔyΔx不存在,则函数 y=f(x)在 x=x0 处不可导. (2)位移函数在某一时刻的瞬时变化率(导数)叫瞬时速度,即 v=lim ΔsΔt=lim s(t0+Δt)-s(t0)Δt. (3)f′(x0)=lim f(x)-f(x0)x-x0与定义中的 f′(x0)意义本质相同. 题型一 物体运动的瞬时速度 【例 1】 一质点按规律 s(t)=at2+1 作直线运动(位移单位:m,时间单位:s),若该质点在 t=2 s 时的瞬时速度为 8 m/s,求常数 a 的值. [思路探索] 求物体的瞬时速度,应先求出平均速度ΔsΔt,再取极限. 解 Δs=s(2+Δt)-s(2) =a(2+Δt)2+1-a·22-1 =4aΔt+aΔt2, ∴ΔsΔt=4a+aΔt. 在 t=2 s 时,瞬时速度为 ΔsΔt=4a,即 4a=8,∴a=2. 规律方法 求瞬时速度是利用平均速度“逐渐逼近”的方法得到的,其求解步骤如下: (1)由物体运动的位移 s 与时间 t 的函数关系式求出位移增量Δs=s(t0+Δt)-s(t0); (2)求时间...