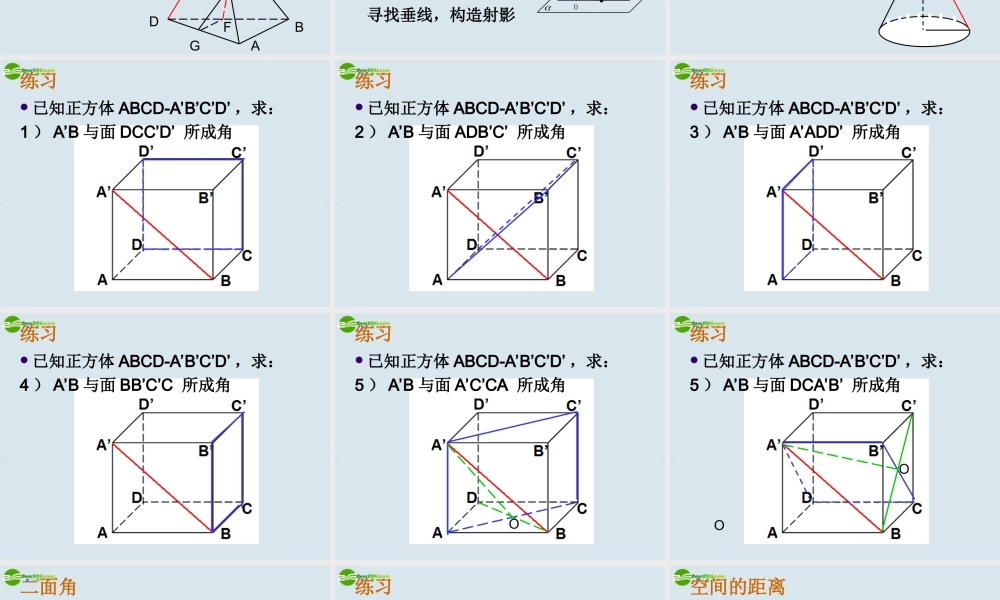
两直线的夹角 等角定理:如果两个角的对边对应平行,则这两个角相等或互补 两异面直线所成的角 定义直线 a , b 是异面直线,过空间任意点O ,分别引直线 a’//a , b’//b ,则 a ’ 和b’ 所成的锐角或直角叫异面直线 a , b 所成的角 范围 解题思路 : 平移 b ' a ' O a b 90,0练习正方体 ABCD-A’B’C’D’ 中, E,F,G分别是 AB , AD , DD’ 的中点,求:1 ) AC 和 A’D 所成角的大小2 ) A’C’ 和 EF 所成角的大小3 ) B’E 和 CG 所成角的大小练习 在三棱锥 C-ABD 中, E 、 F 分别是 AC 和 DB 的中点,若 CD=2AB=4 , EFAB⊥,求 EF 和 CD 所成角的大小DABCGEF直线与平面所成的角(线面角) 定义:平面的斜线和它在面内的射影所成的锐角。 规定:线面垂直时,线面角是直角; 线面平行时,线面角是 0°角。 范围: 解题思路: 寻找垂线,构造射影 90,0 B O A a 练习已知圆锥母线长为 4 ,底面半径为 2 ,求母线和底面所成的角练习 已知正方体 ABCD-A’B’C’D’ ,求:1 ) A’B 与面 DCC’D’ 所成角练习 已知正方体 ABCD-A’B’C’D’ ,求:2 ) A’B 与面 ADB’C’ 所成角练习 已知正方体 ABCD-A’B’C’D’ ,求:3 ) A’B 与面 A’ADD’ 所成角练习 已知正方体 ABCD-A’B’C’D’ ,求:4 ) A’B 与面 BB’C’C 所成角练习 已知正方体 ABCD-A’B’C’D’ ,求:5 ) A’B 与面 A’C’CA 所成角O练习 已知正方体 ABCD-A’B’C’D’ ,求:5 ) A’B 与面 DCA’B’ 所成角OO二面角 定义 : 已知二面角 α-l-β ,分别在 α , β 内作 BA⊥l , CA⊥l ,则∠ BAC 叫二面角 α-l-β 的平面角。 范围 求法① 定义法:在二面角的棱上取一点(特殊点),在两个半平面内分别做垂直于棱的射线,得到二面角的平面角② 三垂线法:由一个半面内一点作(或找)到另一个半平面的垂线,过垂足做棱垂线,连接棱垂线的垂足和点,构造二面角的平面角,再求解③ 垂面法:过棱上一点做垂直于棱的平面与两个半平面相交,两条交线所成的角即为二面角的平面角 A C B 180,0练习已知正方体 ABCD-A’B’C’D’ , E,F分别是棱 BC , CC’ 的中点,求:1 )面 ABC’D’ ...