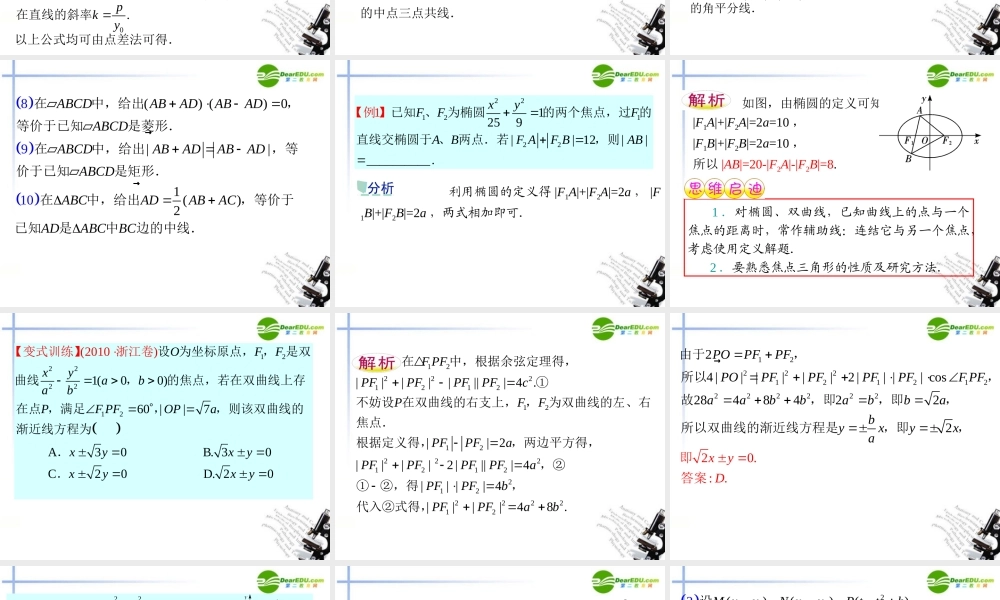
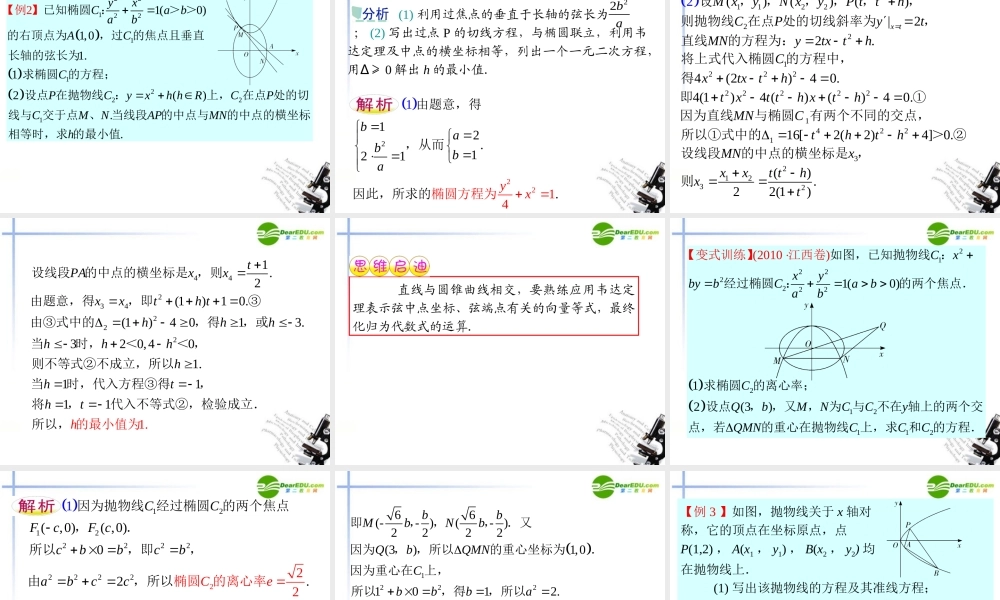
专题五 解析几何 2222222222222222221(0)cos()sin1(0)1(00)1(12300)2(0)2(0)1xyxababxayybyxababxyxababyxyababypx pypx p圆锥曲线的标准方程椭圆:焦点在 轴上时参数方程,其中 为参数 ;焦点在轴上时.双曲线:焦点在 轴上:,;焦点在 轴上:,.抛物线:开口向右时,,开口向左时,.222(0)2(0)xpy pxpy p,开口向上时,开口向下时. 2222222222222222222222222211111(0)123142xyabxyxyababxyabxyxabaybmxny 常用曲线方程设法技巧共焦点的设法:与椭圆有公共焦点的椭圆方程为;与双曲线有公共焦点的双曲线方程为;与双曲线共渐近线的双曲线方程为;中心在原点,对称轴为坐标轴的椭圆、双曲线方程可设为;不清楚开口方向的抛.物线设法:焦22(0)(0)xymx myxmy m点在 轴上,;焦点在 轴上,.2212122221212122||()()|112 | (1)[()4]1 1||3.ABxxyyABkxxkxxx xyyk直线与圆锥曲线相交弦长公式.的或2200222020220022202020001()1()2(0)()4.xyP xyabb xka yxyP xyabb xka yypx pP xypky圆锥曲线中点弦斜率公式在椭圆中,以,为中点的弦所在直线的斜率;在双曲线中,以,为中点的弦所在直线的斜率;在抛物线中,以,为中点的弦所在直线的斜率以上公式均可由点差.法可得. (1)(123)54.0()kmnnkmOAOBABOAOBABPMPNPMNAPAQBPBQABPQ���解析几何与向量综合的有关结论给出直线的方向向量,或, ,等价于已知直线的斜率 或给出与相交,等价于已知过的中点.给出,等价于已知 是的中点.给出,.等价于已知 , 与的中点三点共线.uu 106/ /50ABACABACOCOAOBABCMA MBMAMBAMBMA MBmAMBMA MBm������给出以下情形之一:①;②存在实数 ,使;③若存在实数 , ,且,使,等价于已知 , , 三点共线.给出,等价于已知,即是直角;给出,等价于已知是钝角或反向共线;给出 70()AMBMAMBMPMPAMBMAMB���,等价于已知是锐角或同向共线.给出,等价于已知是的角平分线. 891() ()1 (00||)2ABCDABADABADABCDABCDABADABADABCDABCADABACAD...