温州地区高一数学已知三角函数值求角 人教版0 课件VIP免费

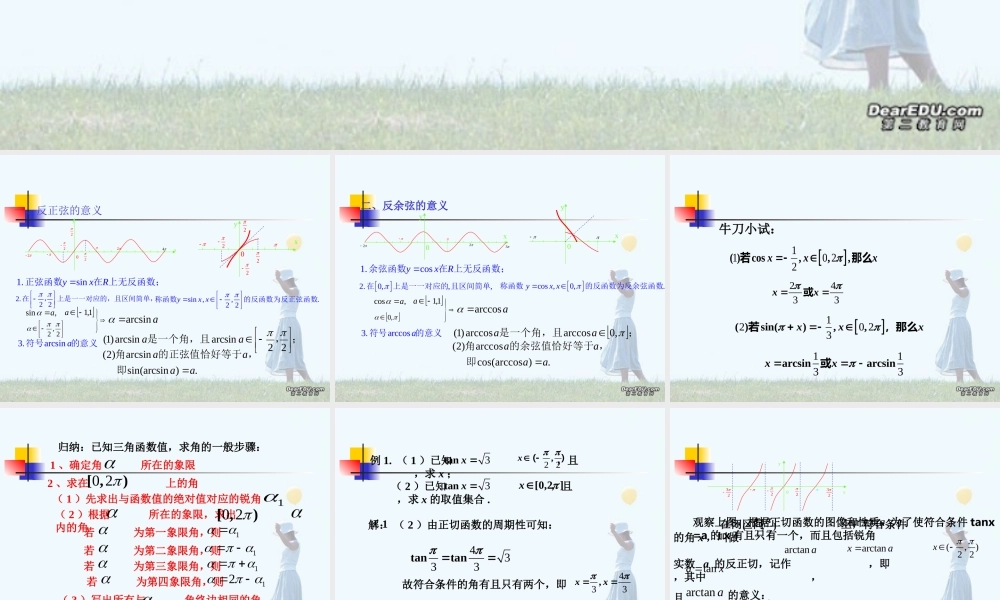
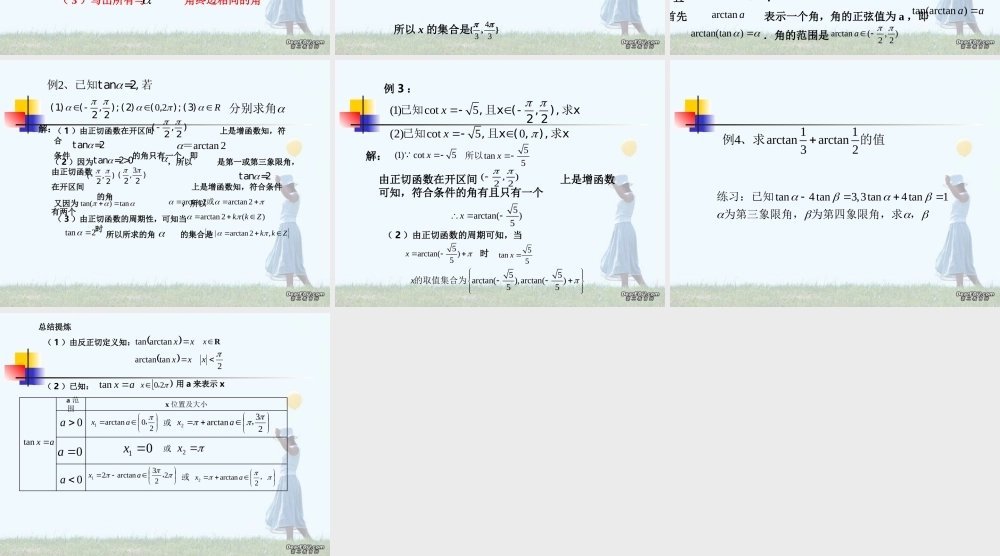
一、反正弦的意义xy02224221.sinyxR正弦函数在 上无反函数；2.2 2 在， 上是一一对应的，且区间简单，sin ,,.2 2yx x  称函数的反函数为反正弦函数,sina1,1a2,2aarcsin3.arcsin a符号的意义；，是一个角，且22arcsinarcsin)1(aa.)sin(arcsinarcsin)2(aaaa即，的正弦值恰好等于角xy02222 二、反余弦的意义1.cosyxR余弦函数在 上无反函数；2.0,,,在上是一一对应的 且区间简单cos ,0,.yx x称函数的反函数为反余弦函数,cosa1,1a,0aarccos3.arccosa符号的意义；是一个角，且,0arccosarccos)1(aa.)cos(arccosarccos)2(aaaa即，的余弦值恰好等于角xy0232xy0 牛刀小试：110 22( )cos,,,xxx若那么120 23( )sin(),,xxx若，那么2433xx或1133arcsinarcsinxx或－ 归纳：已知三角函数值，求角的一般步骤：1 、确定角 所在的象限2 、求在 上的角0 2[ ,)（ 1 ）先求出与函数值的绝对值对应的锐角1（ 2 ）根据 所在的象限，求出 内的角0 2[ ,)若 为第一象限角，则1若 为第二象限角，则1 若 为第三象限角，则1 若 为第四象限角，则12（ 3 ）写出所有与 角终边相同的角 例 1. （ 1 ）已知 ，且 ，求 x ； 3tan x 2 2,x  （）（ 2 ）已知 ，且 ，求 x 的取值集合 . ]2,0[x3tan x 解：可知符合条件的角有且只有一个，即 ． （ 1 ）由于正弦函数在闭区间 上是增函数和2 2(,) 33tan  3于是3x（ 2 ）由正切函数的周期性可知：所以 x 的集合是433{,}4333tantan故符合条件的角有且只有两个，即433,xx 0yx322232 在闭区间 上，符合条件 的角 x ，叫做实数 a 的反正切，记作 ，即 ，其中 ，且 ．2 2(,) tan xaarctan aarctanxa(,)2 2x  tanax观察上图，根据正切函数的图像和性质，为了使符合条件 tanx=a 的 x 有且只有一个，而且包括锐角arctan a 的意义：首先 表示一个角，角的正弦值为 a ，即．角的范围是arctan...