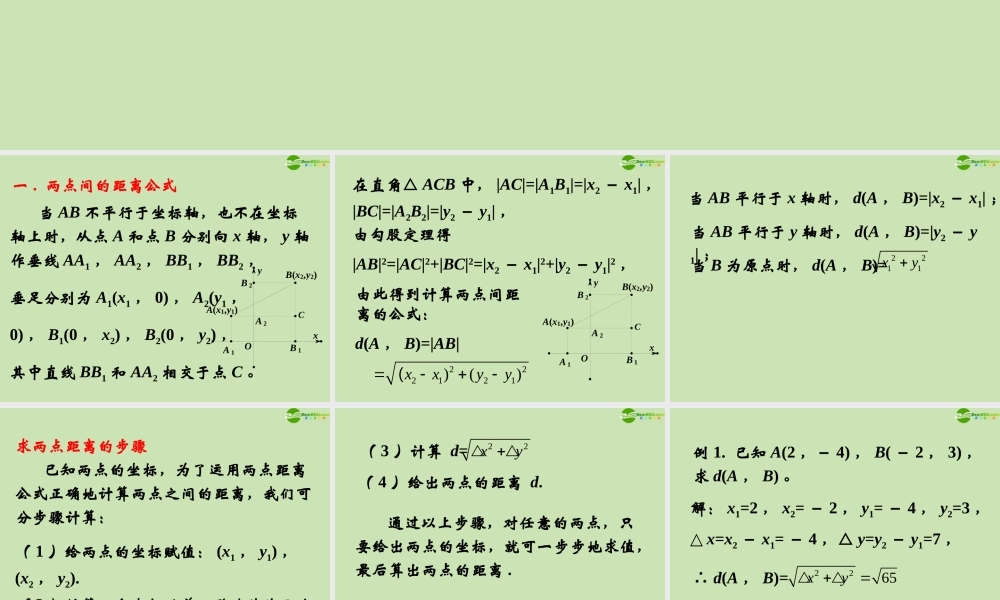
2.1.2 平面直角坐标系中的 基本公式 一 . 两点间的距离公式 当 AB 不平行于坐标轴,也不在坐标轴上时,从点 A 和点 B 分别向 x 轴, y 轴作垂线 AA1 , AA2 , BB1 , BB2 ,垂足分别为 A1(x1 , 0) , A2(y1 ,0) , B1(0 , x2) , B2(0 , y2) ,其中直线 BB1 和 AA2 相交于点 C 。 B 2B 1A 2A 1B(x2,y2)A(x1,y1)OyxC 在直角△ ACB 中, |AC|=|A1B1|=|x2 - x1| ,|BC|=|A2B2|=|y2 - y1| ,B 2B 1A 2A 1B(x2,y2)A(x1,y1)OyxC由勾股定理得|AB|2=|AC|2+|BC|2=|x2 - x1|2+|y2 - y1|2 ,由此得到计算两点间距离的公式:d(A , B)=|AB|222121)()xxyy( 当 AB 平行于 x 轴时, d(A , B)=|x2 - x1| ; 当 AB 平行于 y 轴时, d(A , B)=|y2 - y1| ;当 B 为原点时, d(A , B)=2211xy 求两点距离的步骤 已知两点的坐标,为了运用两点距离公式正确地计算两点之间的距离,我们可分步骤计算:( 1 )给两点的坐标赋值: (x1 , y1) ,(x2 , y2).( 2 )计算两个坐标的差,并赋值给另外两个变量,即△ x=x2 - x1 ,△ y=y2 - y1. ( 3 )计算 d=22xy( 4 )给出两点的距离 d. 通过以上步骤,对任意的两点,只要给出两点的坐标,就可一步步地求值,最后算出两点的距离 . 例 1. 已知 A(2 ,- 4) , B( - 2 , 3) ,求 d(A , B) 。解: x1=2 , x2= - 2 , y1= - 4 , y2=3 ,△ x=x2 - x1= - 4 ,△ y=y2 - y1=7 , ∴ d(A , B)=2265xy 例 2 .已知点 A(1 , 2) , B(3 , 4) , C(5 ,0), 求证:△ ABC 是等腰三角形。证明:因为 d(A , B)= 22(3 1)(42)8d(A , C)= 225 10220() ()d(B , C)= 22530420() ()因为 |AC|=|BC| ,且 A , B , C 不共线, 所以△ ABC 是等腰三角形。 二 . 坐标法 坐标法:就是通过建立坐标系(直线坐标系或者是直角坐标系),将几何问题转化为代数问题,再通过一步步地计算来解决问题的方法 .用坐标法证题的步骤 用坐标法证题的步骤( 1 )根据题设条件,在适当位置建立坐标系(直线坐标系或者是直角坐标系);( 2 )设出未知坐标;( 3 )根据题设条件推导出所需未知点的坐标,进而推导结论 . 例 3 .已...