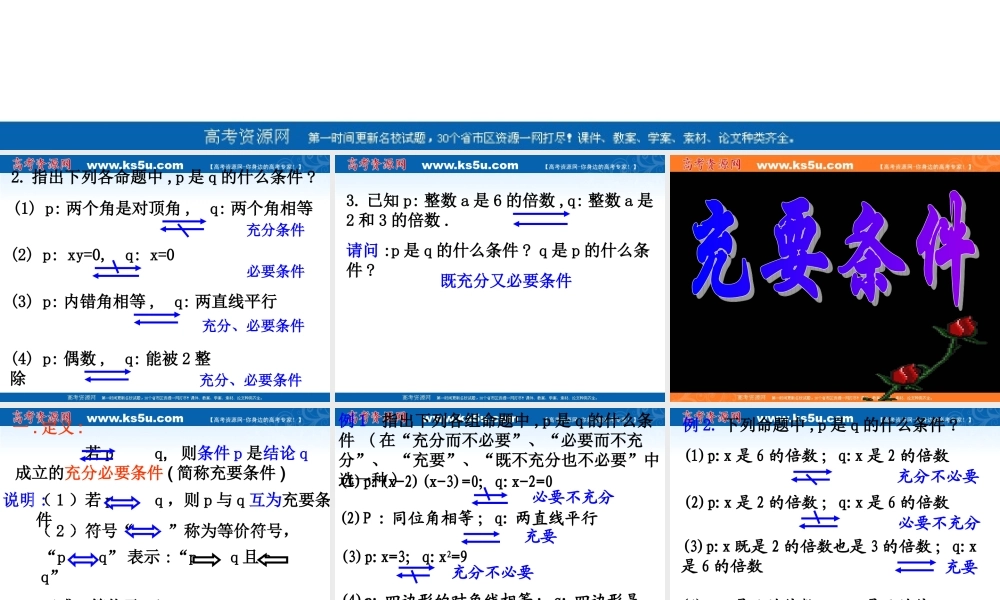
1. 如何理解 : (1) p 是 q 的充分条件复习提问 :由条件 p 结论 q,(2) p 是 q 的必要条件由结论 q 条件p,则条件 p 是结论 q 成立的充分条件 ;则条件 p 是结论成立的必要条件 2. 指出下列各命题中 ,p 是 q 的什么条件 ?(1) p: 两个角是对顶角 , q: 两个角相等充分条件(2) p: xy=0, q: x=0必要条件(3) p: 内错角相等 , q: 两直线平行充分、必要条件(4) p: 偶数 , q: 能被 2 整除充分、必要条件 3. 已知 p: 整数 a 是 6 的倍数 ,q: 整数 a 是2 和 3 的倍数 .请问 :p 是 q 的什么条件 ? q 是 p 的什么条件 ?既充分又必要条件 一 . 定义 : 若 p q, 则条件 p 是结论 q成立的充分必要条件 ( 简称充要条件 )说明 :“p q” 表示 :“p q 且 p q”(或 p 等价于 q )( 2 )符号“ ”称为等价符号,( 1 )若 p q ,则 p 与 q 互为充要条件二 . 如何判断命题中的条件是结论的充要条件 例 1 指出下列各组命题中 ,p 是 q 的什么条件 ( 在“充分而不必要”、“必要而不充分”、 “充要”、“既不充分也不必要”中选一种 )(1)p:(x-2)(x-3)=0; q:x-2=0(2)P : 同位角相等 ; q: 两直线平行(3)p:x=3; q:x2=9(4)p: 四边形的对角线相等 ; q: 四边形是平行四边形必要不充分充要充分不必要既不充分又不必要 (1)p:x 是 6 的倍数 ; q:x 是 2 的倍数(2)p:x 是 2 的倍数 ; q:x 是 6 的倍数(3)p:x 既是 2 的倍数也是 3 的倍数 ; q:x是 6 的倍数(4)p:x 是 4 的倍数 ; q:x 是 6 的倍数充分不必要必要不充分充要既不充分又不必要例 2. 下列命题中 ,p 是 q 的什么条件 ? 例 3. 下列命题中 , 哪些 p 是 q 的充要条件 ?(1)p:b=0, q: 函数 f(x)=ax2+bx+c 是偶函数(2)p: x>0,y>0, q:xy>0(3)p:a>b, q:a+c>b+c充要条件充分不必要充要条件故选 (1)(2) 例 4. 已知 : 圆 O 的半径 r, 圆心 O 到直线 l 的距离为 d, 求证 :d=r 是直线 l 与圆 O 相切的充要条件需分别证明(1)充分性( p q ); (2)必要性(q p )证明:如图,作 OP l 于点 P ,则 OP = d .设 p:d=r, q: 直线 l 与圆 O 相切分析 :lQP0┐d (1) 充分性( p q ) : 若 d=r, 则点 P 在圆 O 上。在直线 l 上任取一点 Q( 异于点 P), 连接 OQ ...