高中数学 112 导数的概念课件 新人教A版选修2-2 课件VIP免费

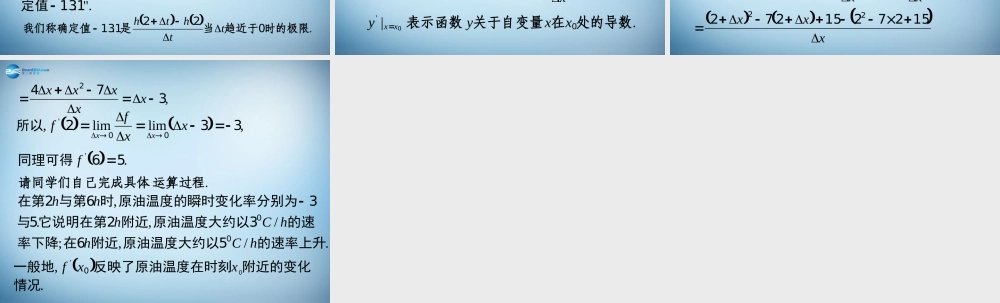
1.1.2 导数的概念?,?,.).tan(.,时的瞬时速度是多少比如度呢如何求运动员的瞬时速那么度在某时刻的瞬时速她他度不一定能反映运动员的平均速的速度称为我们把物体在某一时刻是不同的度运动员在不同时刻的速在高台跳水运动中2tvelociyeousins瞬时速度.,,,.,;,.,,,,,.可以得到如下表格内平均速度和区间计算区间之后在时当之前在时当但不为也可以是负值正值可以是是时间的改变量任意取一个时刻之前或之后在附近的情况我们先考察vtttttttttt22222202200222 tthhvtt2222220这段时间内在时,,ttt113942..11394..t;.,.05113010vt时当;.,.0951130010vt时当;.,.099511300010vt时当;.,.09995113000010vt时当;.,.0999951130000010vt时当  2222220ththvtt这段时间内在时,,ttt113942..11394..t;.,.14913010vt时当;.,.1049130010vt时当;.,.100491300010vt时当;.,.10004913000010vt时当;.,.1000049130000010vt时当?,有什么样的变化趋势平均速度时趋近于当观察vt0..,,,,1132220个确定的值平均速度都趋近于一时一边趋近于还是从大于的一边从小于即无论时趋近于当我们发现tt./.,.,||,smttvt11322时的瞬时速度是员在运动因此时的瞬时速度就无限趋近于速度平均无限变小时时间间隔从物理的角度看 "..,,".lim,11302113220定值趋近于确平均速度时趋势近于当表示我们用为了表述方便vttththt ..时的极限趋近于当是我们称确定值022113tthth ?.?.示处的瞬时变化率怎样表在函数的瞬时速度怎样表示运动员在某时刻探究0021xxxft  .lim|''xxfxxfyxfxxx0000 即或记作   ,,limlim,derivativexxxfyxfxxfxxfxxxfyxx处的在我们称它为函数处的瞬时变化率是在函数一般地000000导数.|'处的导数在关于自变量表示函数00xxyyxx .,,).(:,.,并说明它们的意义的瞬时变化率原油温度时和第计算第为单位的温度原油时如果在和加热行冷却油进对原需要品产柴油、塑胶等各种不同将原油精炼为汽油、例hhxxxxfCxh6280157120...