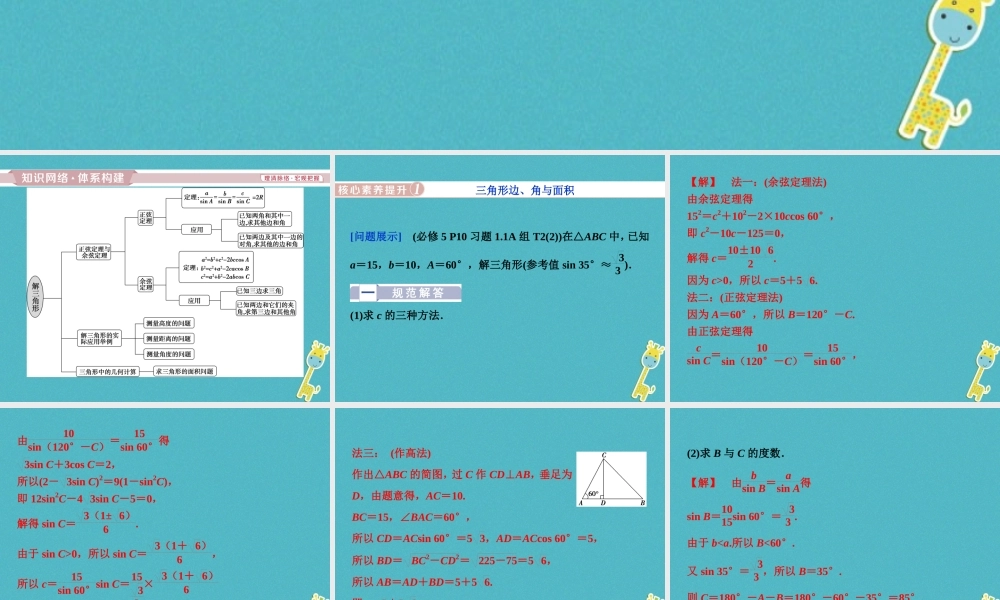
章末复习提升课 第一章 解三角形 [问题展示] (必修 5 P10 习题 1.1A 组 T2(2))在△ABC 中,已知a=15,b=10,A=60°,解三角形(参考值 sin 35°≈ 33 ). (1)求 c 的三种方法. 三角形边、角与面积【解】 法一:(余弦定理法) 由余弦定理得 152=c2+102-2×10ccos 60°, 即 c2-10c-125=0, 解得 c=10±10 62. 因为 c>0,所以 c=5+5 6. 法二:(正弦定理法) 因为 A=60°,所以 B=120°-C. 由正弦定理得 csin C=10sin(120°-C)=15sin 60°, 由10sin(120°-C)=15sin 60°得 3sin C+3cos C=2, 所以(2- 3sin C)2=9(1-sin2C), 即 12sin2C-4 3sin C-5=0, 解得 sin C= 3(1± 6)6. 由于 sin C>0,所以 sin C= 3(1+ 6)6, 所以 c=15sin 60°sin C=1532× 3(1+ 6)6 =5+5 6. 法三: (作高法) 作出△ABC 的简图,过 C 作 CD⊥AB,垂足为D,由题意得,AC=10. BC=15,∠BAC=60°, 所以 CD=ACsin 60°=5 3,AD=ACcos 60°=5, 所以 BD= BC2-CD2= 225-75=5 6, 所以 AB=AD+BD=5+5 6. 即 c=5+5 6. (2)求 B 与 C 的度数. 【解】 由bsin B=asin A得 sin B=1015sin 60°= 33 . 由于 b
0. 所以 cos A=12,又 0