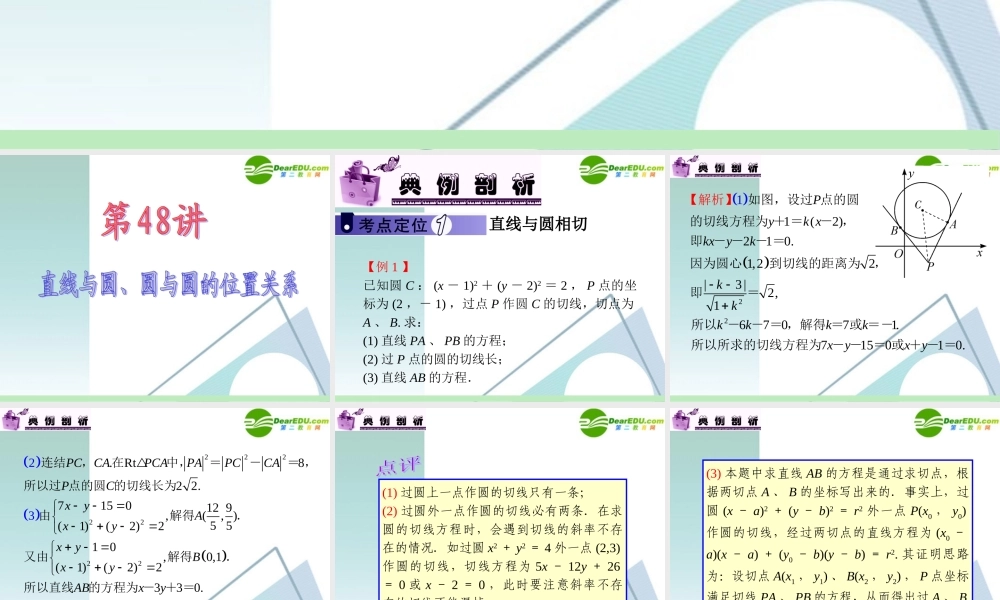
直线与圆相切 【例 1 】已知圆 C : (x - 1)2 + (y - 2)2 = 2 , P 点的坐标为 (2 ,- 1) ,过点 P 作圆 C 的切线,切点为A 、 B. 求:(1) 直线 PA 、 PB 的方程;(2) 过 P 点的圆的切线长;(3) 直线 AB 的方程. 221(2)210.1,22|3|2,167071.7150.110Pyk xkxykkkkkkkxyxy如图,设过 点的圆的切线方程为 + =- ,即 - -- =因为圆心到切线的距离为,即=所以 -- = ,解得 = 或 =-所以所求的切线方程为 - -= 或 +【-】=解析 2222222.Rt82 2.715012 9,(, )5 5(1)(2)210,0,1(1)(2)233.230PCCAPCAPAPCCAPCxyAxyxyBxyABxy连结,在中,=-= ,所以过 点的圆 的切线长为由解得.又由解得.所以直线的方程为 - + =(1) 过圆上一点作圆的切线只有一条;(2) 过圆外一点作圆的切线必有两条.在求圆的切线方程时,会遇到切线的斜率不存在的情况.如过圆 x2 + y2 = 4 外一点 (2,3)作圆的切线,切线方程为 5x - 12y + 26= 0 或 x - 2 = 0 ,此时要注意斜率不存在的切线不能漏掉;(3) 本题中求直线 AB 的方程是通过求切点,根据两切点 A 、 B 的坐标写出来的.事实上,过圆 (x - a)2 + (y - b)2 = r2 外一点 P(x0 , y0)作圆的切线,经过两切点的直线方程为 (x0 -a)(x - a) + (y0 - b)(y - b) = r2. 其证明思路为:设切点 A(x1 , y1) 、 B(x2 , y2) , P 点坐标满足切线 PA 、 PB 的方程,从而得出过 A 、 B两点的直线方程. 22(2)114 223MxyQxQAQBMABQAMBABMQ已知圆: + -= , 是 轴上的动点,、分别切圆于 , 两点.求四边【变式练形的面积的最小值;若=,求习1】直线的方程. 22222222·1132 211331Rt13.3,0295(5 0)252 5 0252 510.2MAQBMAAQSMA QAQAMQMAMQMQABMQPMPABMBBQMPMBQMBMP MQMQMQQ xxxQMQxyxy 四边形因为,所以=====设与交于点 ,则,,==在中,=,即 =,所以=设,则 + = , =,,所以,,所以直线的方程为 +-= 或】-+析=【解【例 2 】已知圆 C : x2 + (y - 1)2 = 5 ,直线 l : mx - y +1 - m = 0.(1) 求证:对任意 m∈R ,直线...