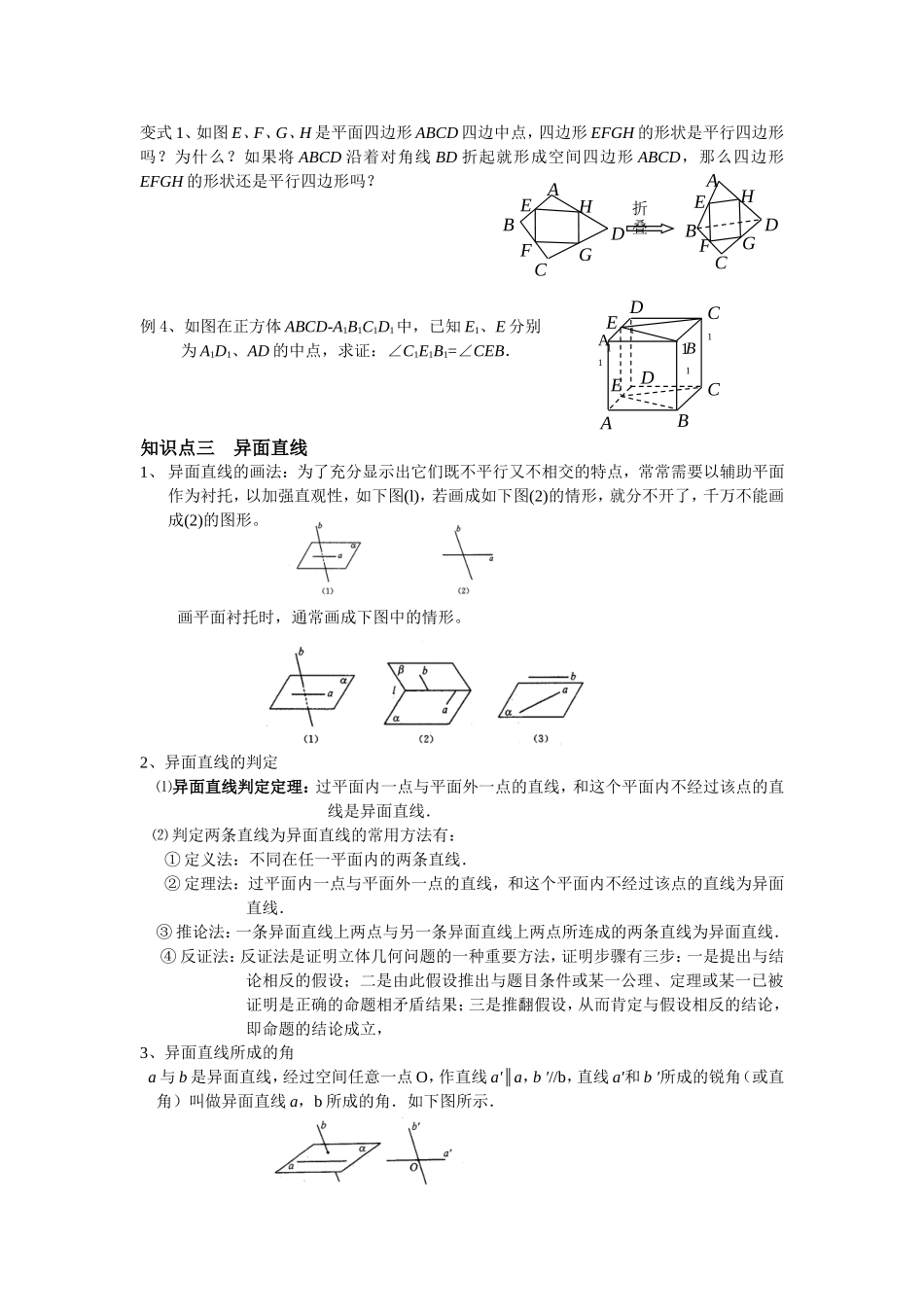
空间两条直线的位置关系知识点一 空间两条直线的位置关系1.异面直线 ⑴ 定义:不同在任何一个平面内的两直线叫做异面直线。 ⑵ 特点:既不相交,也不平行。⑶ 理解:①“不同在任何一个平面内”,指这两条直线永不具备确定平面的条件,因此,异面直线既不相交,也不平行,要注意把握异面直线的不共面性。②“不同在任……”也可以理解为“任何一个平面都不可能同时经过这两条直线”。③ 不能把异面直线误解为分别在不同平面内的两条直线为异面直线.也就是说,在两个不同平面内的直线,它们既可以是平行直线,也可以是相交直线.2.空间两条直线的位置关系 ⑴ 相交——在同一平面内,有且只有一个公共点; ⑵ 平行——在同一平面内,没有公共点; ⑶ 异面——不同在任何个平面内,没有公共点.例 1、正方体 ABCD-A1B1C1D1 中,M、N 分别为棱 C1D1、C1C 的中点,有以下四个结论: ① 直线 AM 与 CC1 是相交直线; ②直线 AM 与 BN 是平行直线;③ 直线 BN 与 MB1 是异面直线; ④直线 AM 与 DD1 是异面直线.其中正确的结论为________.(注:把你认为正确的结论的序号都填上)答案:③④例 2、异面直线是指____. ① 空间中两条不相交的直线; ②分别位于两个不同平面内的两条直线; ③ 平面内的一条直线与平面外的一条直线;④不同在任何一个平面内的两条直线.变式 1、一个正方体中共有 对异面直线.知识点二 平行直线1.公理 4 :平行于同一条直线的两条直线互相平行.符号表示: 2.等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等. 例 3、如图在长方体 ABCD-A1B1C1D1中,已知 E、F 分别为AB、BC 的中点,求证:EF∥A1C1.a∥bb∥cÞa∥cABCDB11A1C1B1D1ABCDEF变式 1、如图 E、F、G、H 是平面四边形 ABCD 四边中点,四边形 EFGH 的形状是平行四边形吗?为什么?如果将 ABCD 沿着对角线 BD 折起就形成空间四边形 ABCD,那么四边形EFGH 的形状还是平行四边形吗?例 4、如图在正方体 ABCD-A1B1C1D1中,已知 E1、E 分别为 A1D1、AD 的中点,求证:∠C1E1B1=∠CEB.知识点三 异面直线1、 异面直线的画法:为了充分显示出它们既不平行又不相交的特点,常常需要以辅助平面作为衬托,以加强直观性,如下图(l),若画成如下图(2)的情形,就分不开了,千万不能画成(2)的图形。画平面衬托时,通常画成下图中的情形。2、异面直线的判定 ...