线段的垂直平分线-VIP免费

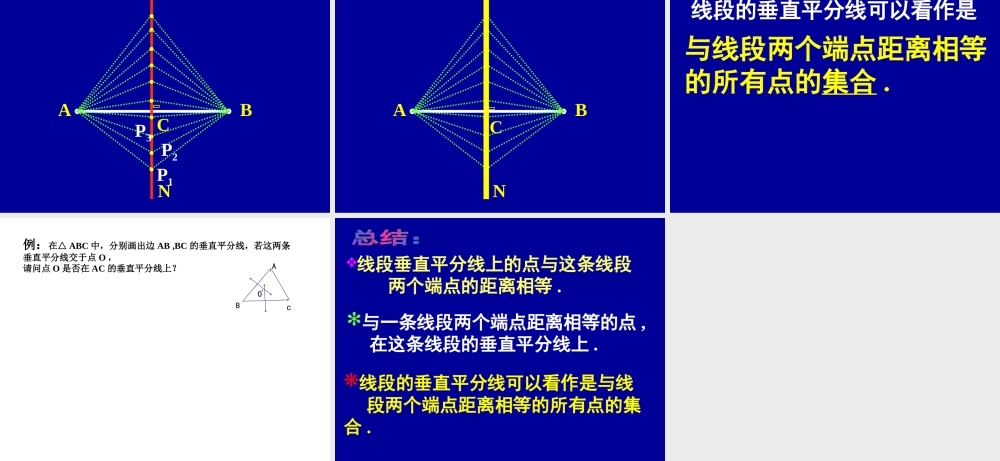
线段的垂直平分线线段的垂直平分线运送球比赛中的思考 运送球比赛中的思考 PABCllCABQ线段垂直平分线上的点与这条线段两个端点的距离相等 .猜 想： 直线 MN⊥AB ，垂足是 C ，且 AC=CB. 点 P 在 MN上 .已知：PA=PB求证：ABCNMP证明 : MN⊥ AB （已知）∴∠PCA= ∠ PCB=90° ( 垂直的定义 )在⊿ PCA 和⊿ PCB 中 ,AC=BC∠ PCA=∠ PCBPC=PC∴ ⊿ PCA ≌ ⊿ PCB(SAS) ∴PA=PB( 全等三角形的对应边相等 )ABCMNP性质：线段垂直平分线上的点与这条线段两个端点的 距离相等。线段的垂直平分线ABPMNCPA=PB点 P 在线段 AB 的垂直平分线上线段垂直平分线上的点到这条线段两个端点的距离相等几何语言叙述 : 点 P 在线段 AB 的垂直平分线上 ∴ PA=PBl已知 :PA=PB想一想：求证：点 P 在线段 AB 的垂直平分线上ABP分析：方法一：过点 P 作 PC⊥AB ，垂足为 C, 然后证明点 C 是 AB 的中点。 方法二：取 AB 的中点 C 并连接 PC, 然后证明点 PC⊥AB 。 ABCPABCP二、合作探究如果 PA=PB ，那么点 P 是否在线段 AB 的垂直平分线上呢？ 已知： PA=PB求证：点 P 在线段 AB 的垂直平分线上方法一：过点 P 作 PC⊥AB ，垂足为 C, 然后证明点 C 是 AB 的中点。 ABCP证明：过点 P 作 PC⊥AB ，垂足为 C在 Rt△APC 和 Rt△BPC 中 ∴ ∠PCA= ∠PCB=90 ° PA=PB PC ＝ PC∴Rt△APC≌Rt△BPC (HL)∴ AC=BC又 PC⊥AB∴ PC 是线段 AB 的垂直平分线即点 P 在线段 AB 的垂直平分线上 已知： PA=PB求证：点 P 在线段 AB 的垂直平分线上方法二：取 AB 的中点 C 并连接 PC, 然后证明 PC⊥AB证明：取 AB 的中点 C 并连接 PC在△ APC 和△ BPC 中 ∴ AC=BC PA=PB AC=BC PC ＝ PC∴Rt△APC≌Rt△BPC (HL)∴ ∠PCA= ∠PCB又 ∠ PCA+∠PCB=180°∴ PC 是线段 AB 的垂直平分线即点 P 在线段 AB 的垂直平分线上 ABCP∴ ∠PCA= ∠PCB=90 °即 PC⊥AB ，垂足为点 C 又 C 是 AB 的中点 线段的垂直平分线ABPC判定：与一条线段两个端点距离相等的点，在这条线段的垂直平分线上。PA=PB点 P 在线段 AB 的垂直平分线上 几何语言叙述 : PA=PB∴ 点 P 在线段 AB 的垂直平分线上小结 :1. 线段的垂直平分线上的点 , 与这条线段两个端点的距离相等 .2. 与一条线段两个端...