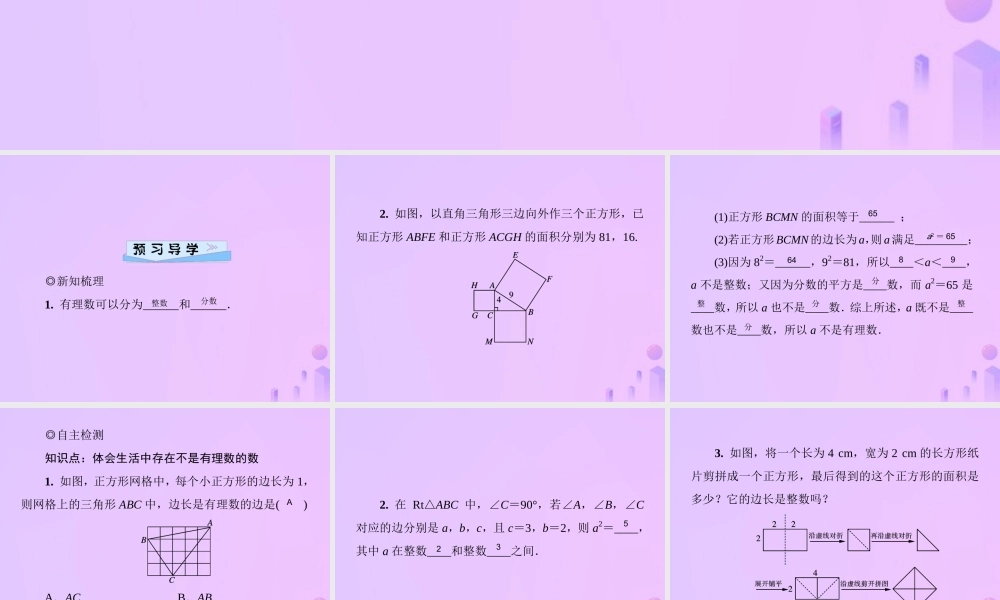
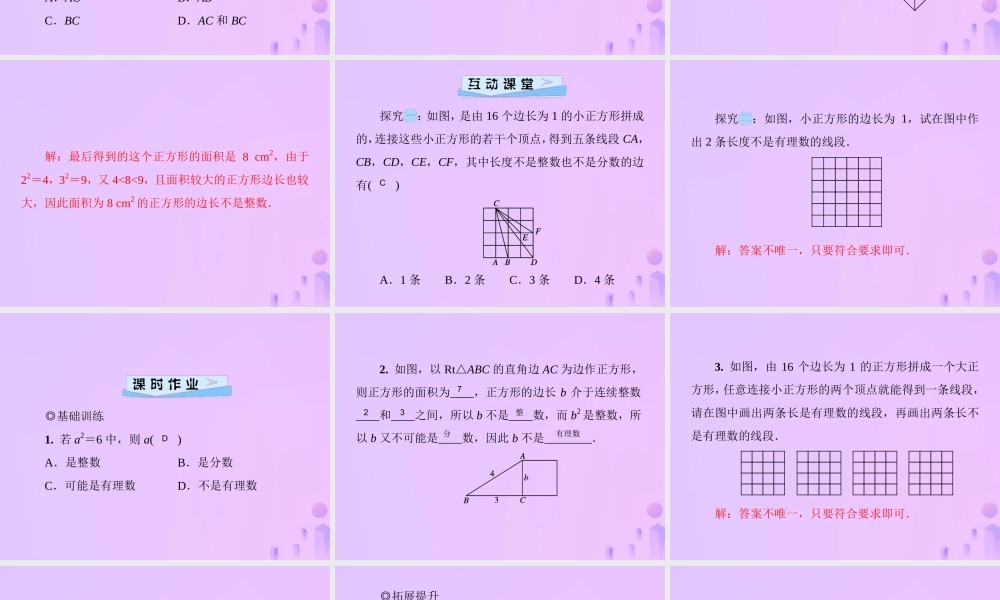
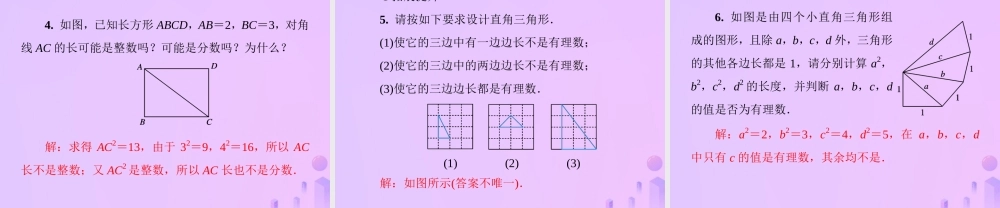
第二章 实数2.1 认识无理数第 1 课时 有理数 ◎新知梳理 1. 有理数可以分为______和______. 整数分数2. 如图,以直角三角形三边向外作三个正方形,已知正方形 ABFE 和正方形 ACGH 的面积分别为 81,16. (1)正方形 BCMN 的面积等于______ ; (2)若正方形 BCMN 的边长为 a,则 a 满足_________; (3)因为 82=______,92=81,所以____<a<____,a 不是整数;又因为分数的平方是____数,而 a2=65 是____数,所以 a 也不是____数.综上所述,a 既不是____数也不是____数,所以 a 不是有理数. 65a2 = 656489分整分整分◎自主检测 知识点:体会生活中存在不是有理数的数 1. 如图,正方形网格中,每个小正方形的边长为 1,则网格上的三角形 ABC 中,边长是有理数的边是( ) A.AC B.AB C.BC D.AC 和 BC A2. 在 Rt△ABC 中,∠C=90°,若∠A,∠B,∠C对应的边分别是 a,b,c,且 c=3,b=2,则 a2=____,其中 a 在整数____和整数____之间. 5233. 如图,将一个长为 4 cm,宽为 2 cm 的长方形纸片剪拼成一个正方形,最后得到的这个正方形的面积是多少?它的边长是整数吗? 解:最后得到的这个正方形的面积是 8 cm2,由于22=4,32=9,又 4<8<9,且面积较大的正方形边长也较大,因此面积为 8 cm2 的正方形的边长不是整数. 探究:如图,是由 16 个边长为 1 的小正方形拼成的,连接这些小正方形的若干个顶点,得到五条线段 CA,CB,CD,CE,CF,其中长度不是整数也不是分数的边有( ) A.1 条 B.2 条 C.3 条 D.4 条 C探究:如图,小正方形的边长为 1,试在图中作出 2 条长度不是有理数的线段. 解:答案不唯一,只要符合要求即可. ◎基础训练 1. 若 a2=6 中,则 a( ) A.是整数 B.是分数 C.可能是有理数 D.不是有理数 D2. 如图,以 Rt△ABC 的直角边 AC 为边作正方形,则正方形的面积为____,正方形的边长 b 介于连续整数____和____之间,所以 b 不是____数,而 b2 是整数,所以 b 又不可能是____数,因此 b 不是________. 723整分有理数3. 如图,由 16 个边长为 1 的正方形拼成一个大正方形,任意连接小正方形的两个顶点就能得到一条线段,请在图中画出两条长是有理数的线段,再画出两条长不是有理数的线段. 解:答案不唯一,只要符合要求即可. 4. 如图,已知长方形 ABCD,AB=2,BC=3,对角...