上学期北京市清华附中高一数学平面向量的坐标运算二 课件VIP免费

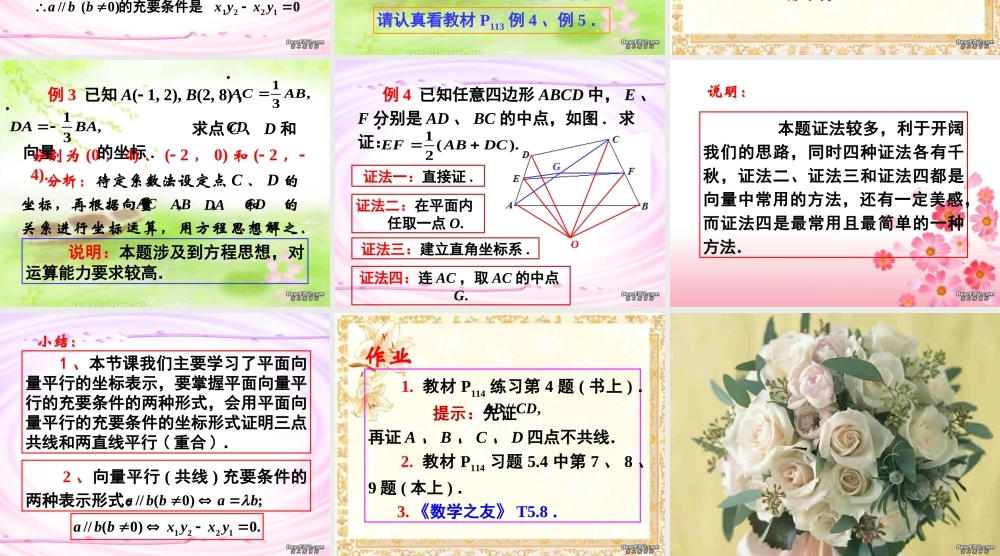
1 、平面向量的坐标表示 :2 、平面向量的坐标运算 :1122((,), ,)axybxy1212 ,abxxyy2121, yyxxba11 (,),axyR其中),( yxjyixa 1 、若 M(3, 2), N(5, 1), 且则点 P 的坐标为 ( ) A ． ( 8 ， 1) B ． ( 1 ， ) C ． (1 ， ) D ． (8 ， 1) 2 、已知 A(0 ， 1) ， B(1 ， 2) ， C(3 ，4) ，则 ____________ ．1,2MPMN�练习：3232( 3 ， 3)B2ABBC� 引进直角坐标系后，向量可以用坐标表示．那么，怎样用坐标反映两个向量的平行？如何用坐标反映平面图形的几何关系？思考：3 、向量平行的坐标表示 :1122(,),(,),0,axybxyb其中可写成ba),,(),(2211yxyx1212.xxyy即12210,x yx y消去 得：0 )0( // 1221yxyxbba的充要条件是设//ab 存在唯一实数，使.ab (1) 消去时不能两式相除 , 因为 y1, y2 有可能为 0. 可分  0 与 = 0讨论．,2211xyxy  (3) 向量平行 ( 共线 ) 充要条件的两种表示形式：(2) 充要条件不能写成 因为 x1, x2 有可能为 0.// (0);ab bab1221// (0)0.ab bx yx y注意：请认真看教材 P113 例 4 、例 5 ． 例 2 已知点 A( 1 ， 1) ， B(1 ，3) ， C(1 ， 5) ， D(2 ， 7) ，向量 与 平行吗？直线 AB 与 CD 平行吗？ 例 1 若向量 = ( 1, x) 与 = ( x, 4) 共线且方向相同，求 x ．aAB�bCD�x = 2.都平行 . 说明：本题涉及到方程思想，对运算能力要求较高． 例 3 已知 A( 1, 2), B(2, 8) ， 求点 C 、 D 和向量 的坐标 .1,3ACAB�1,3DABA�CD� 分析：待定系数法设定点 C 、 D 的坐标，再根据向量 ， ， 和 的关系进行坐标运算，用方程思想解之．AC�CD�AB�DA�分别为 (0 ， 4) 、 ( 2 ， 0) 和 ( 2 ， 4).O 例 4 已知任意四边形 ABCD 中， E 、F 分别是 AD 、 BC 的中点，如图 . 求证：1 ().2EFABDC�证法一：直接证 .证法二：在平面内 任取一点 O.证法三：建立直角坐标系 .证法四：连 AC ，取 AC 的中点G.G 本题证...