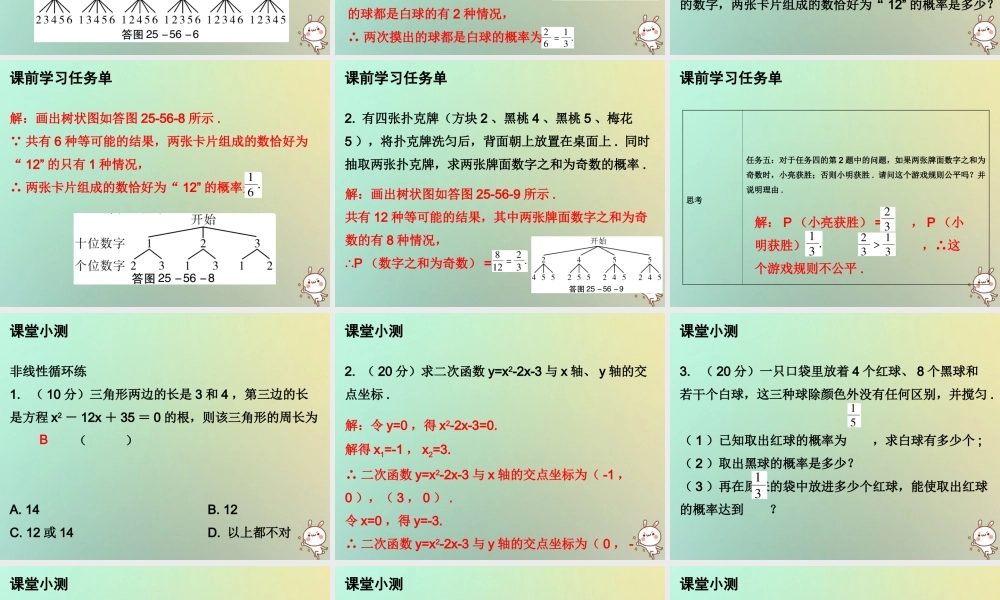
第二十五章概率初步课前学习任务单第 56 课时用列举法求概率( 3 )——无放回型课前学习任务单目标任务一:明确本课时学习目标能够运用列表法或画树状图法计算“无放回型”事件发生的概率,并阐明理由 .承前任务二:复习回顾1. 六张看上去无差别的卡片上分别写有 1~6 的整数,随机抽取一张后不放回,再随机抽取第二张 . 用列表法列出所有可能的结果 .课前学习任务单略 .2. 根据左边所列表格,求下列事件的概率:( 1 )“两数之积是偶数”的概率;( 2 )“两数之和是偶数”的概率 . 课前学习任务单解:( 1 ) ( 2 )启后任务三:学习列举法,完成题目1. 用树状图表示任务二中第 1 题所有可能的结果 .课前学习任务单解:如答图 25-56-6 所示 . 2. 一只不透明的箱子里共有 3 个球,其中 2 个白球、1 个红球,它们除颜色外均相同 . 从箱子中随机摸出一个球,记录下颜色后不将它放回箱子,搅匀后再摸出一个球,求两次摸出的球都是白球的概率 . 课前学习任务单解:画出树状图如答图 25-56-7 所示 . 共有 6 种等可能的结果,两次摸出的球都是白球的有 2 种情况,∴ 两次摸出的球都是白球的概率为范例任务四:运用列表法或画树状图法计算“无放回型”事件发生的概率 1. 将正面分别标有数字 1 , 2 , 3 ,背面花色相同的三张卡片洗匀后,背面朝上放在桌面上 . 随机抽取一张作为个位上的数字(不放回),再抽取一张作为十位上的数字,两张卡片组成的数恰好为“ 12” 的概率是多少?课前学习任务单课前学习任务单解:画出树状图如答图 25-56-8 所示 . 共有 6 种等可能的结果,两张卡片组成的数恰好为“ 12” 的只有 1 种情况,∴ 两张卡片组成的数恰好为“ 12” 的概率是2. 有四张扑克牌(方块 2 、黑桃 4 、黑桃 5 、梅花5 ),将扑克牌洗匀后,背面朝上放置在桌面上 . 同时抽取两张扑克牌,求两张牌面数字之和为奇数的概率 . 课前学习任务单解:画出树状图如答图 25-56-9 所示 .共有 12 种等可能的结果,其中两张牌面数字之和为奇数的有 8 种情况,∴P (数字之和为奇数) =课前学习任务单思考任务五:对于任务四的第 2 题中的问题,如果两张牌面数字之和为奇数时,小亮获胜;否则小明获胜 . 请问这个游戏规则公平吗?并说明理由 . 解: P (小亮获胜) = , P (小明获胜) = ,∴这个游戏规则不公平 .课堂小测非线性循环...