数学 3.2.1立体几何中的向量方法 方向向量与法向量课件 新人教版选修2 1 课件VIP免费

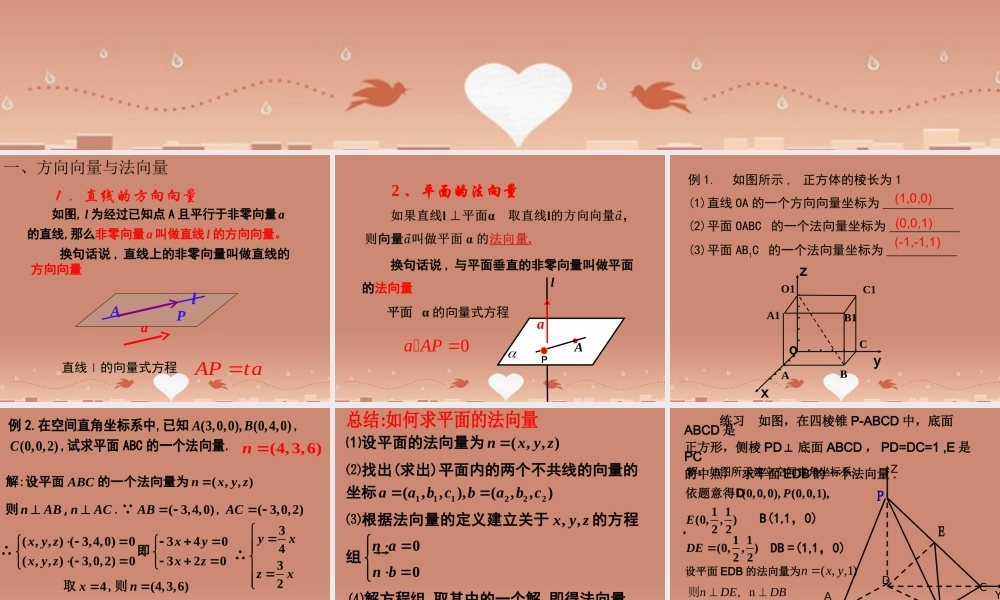
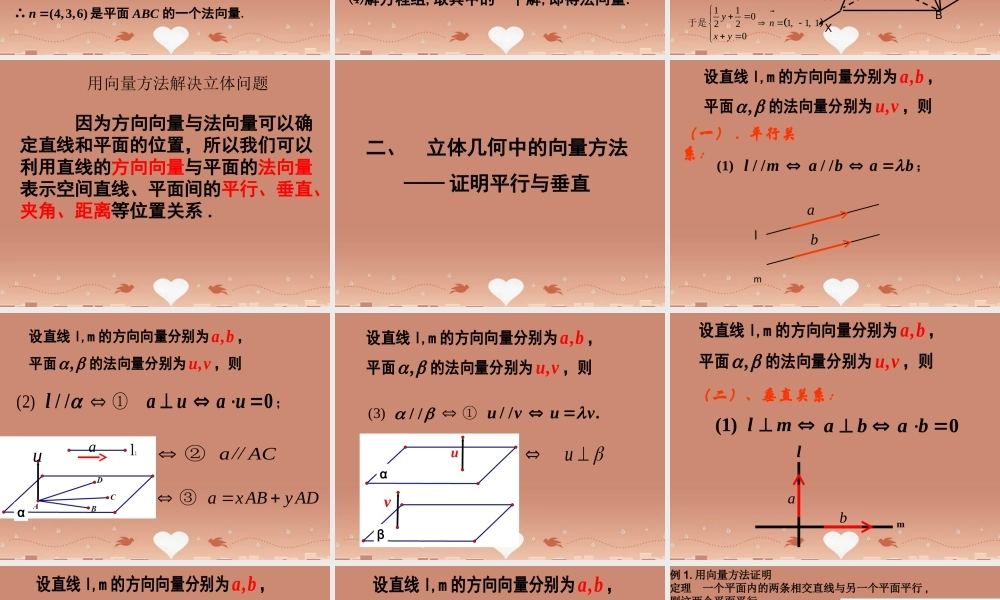
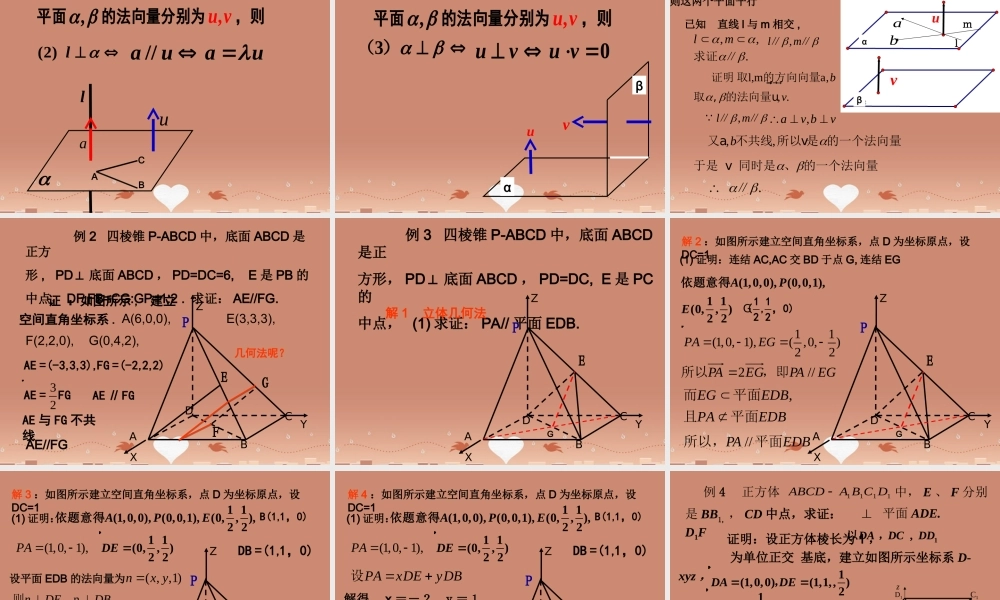
3.2.1 立体几何中的向量方法—— 方向向量与法向量如图, l 为经过已知点 A 且平行于非零向量a 的直线,那么非零向量a叫做直线 l 的方向向量。 lAPa１．直线的方向向量直线ｌ的向量式方程 换句话说 , 直线上的非零向量叫做直线的方向向量APta�一、方向向量与法向量2 、平面的法向量AalP平面 α 的向量式方程0a AP �� 换句话说 , 与平面垂直的非零向量叫做平面的法向量oxyzABCO1A1B1C1例 1. 如图所示 , 正方体的棱长为 1(1)直线 OA 的一个方向向量坐标为 ___________(2)平面 OABC 的一个法向量坐标为 ___________(3)平面 AB1C 的一个法向量坐标为 ___________(-1,-1,1)(0,0,1)(1,0,0)例 2.在空间直角坐标系中,已知(3,0,0),(0,4,0)AB, (0,0,2)C,试求平面 ABC 的一个法向量. (4,3,6)n  解:设平面 ABC 的一个法向量为( , , )nx y z 则 nAB nAC��，. ( 3,4,0)AB  �,( 3,0,2)AC  � ∴ ( , , ) ( 3,4,0)0( , , ) ( 3,0,2)0x y zx y z  即340320xyxz ∴3432yxzx  取4x  ,则(4,3,6)n  ∴(4,3,6)n 是平面 ABC 的一个法向量. 总结:如何求平面的法向量 ⑴设平面的法向量为( , , )nx y z ⑵找出(求出)平面内的两个不共线的向量的坐标111222(,,),(,,)aa b cba b c ⑶根据法向量的定义建立关于, ,x y z 的方程组00n an b    ⑷解方程组,取其中的一个解,即得法向量. 练习 如图，在四棱锥 P-ABCD 中，底面ABCD 是正方形，侧棱 PD⊥ 底面 ABCD ， PD=DC=1 ,E 是PC的中点， 求平面 EDB 的一个法向量 .ABCDPE解：如图所示建立空间直角坐标系 .(0,0,0),(0,0,1),1 1(0,, )2 2PE依题意得DB(1,1，0)1 1(0,, )2 2DE ��DB =(1,1，0)XYZ设平面 EDB 的法向量为( , ,1)nx y, nnDEDB��则1101, 1, 1220ynxy 于是 因为方向向量与法向量可以确定直线和平面的位置，所以我们可以利用直线的方向向量与平面的法向量表示空间直线、平面间的平行、垂直、夹角、距离等位置关系 . 用向量方法解决立体问题二、 立体几何中的向量方法—— 证明平行与垂直设直线 l,m 的方向向量分别为 ,a b， 平面 ,  的法...