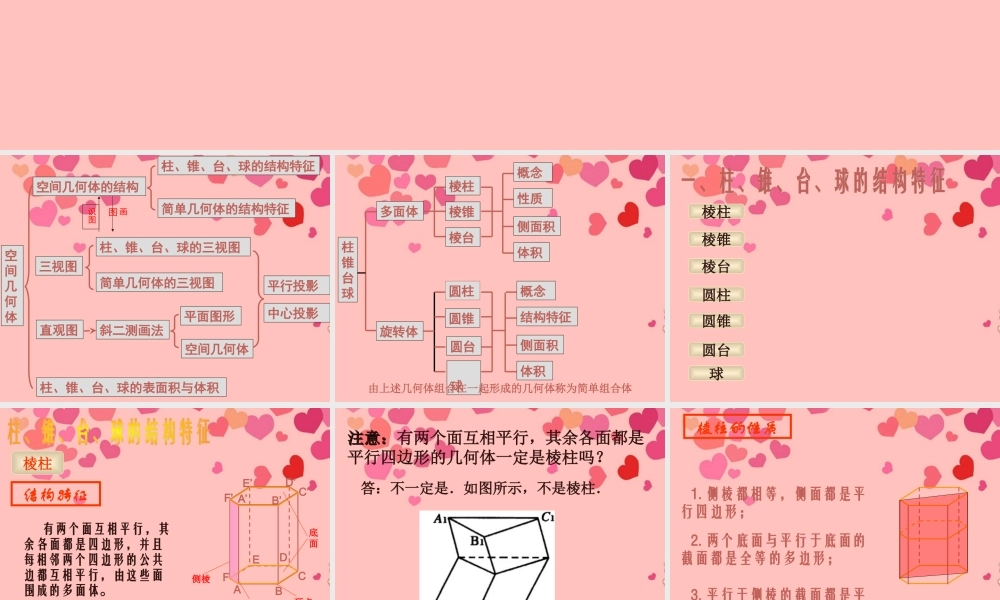
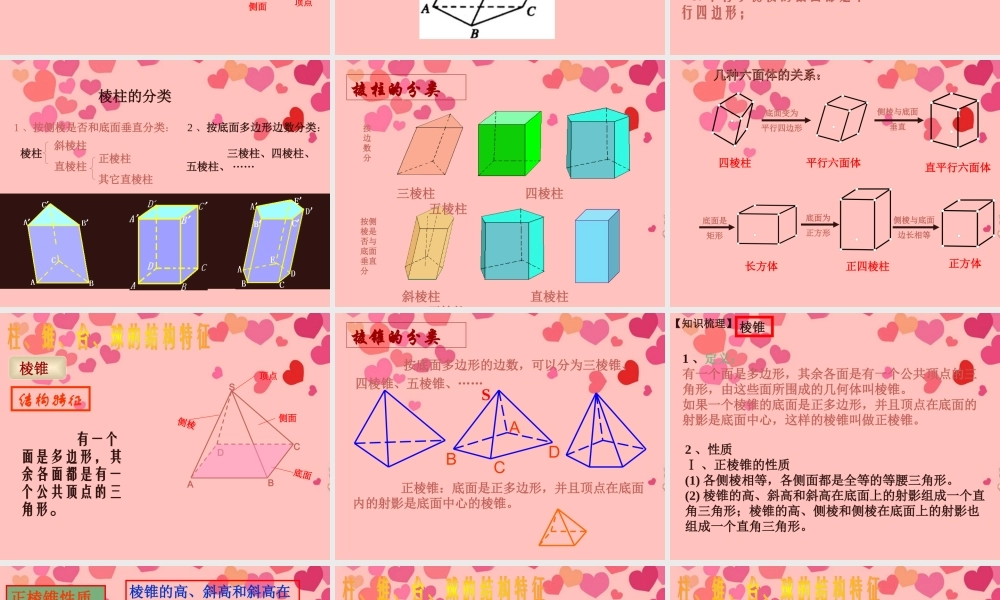
空间几何体空间几何体的结构柱、锥、台、球的结构特征简单几何体的结构特征三视图柱、锥、台、球的三视图简单几何体的三视图直观图斜二测画法平面图形空间几何体中心投影柱、锥、台、球的表面积与体积平行投影画图识图柱锥台球圆锥圆台多面体旋转体圆柱棱柱棱锥棱台概念结构特征侧面积体积 球概念性质侧面积体积由上述几何体组合在一起形成的几何体称为简单组合体棱柱棱锥圆柱圆锥圆台棱台球DABCEFF’ A’E’D’B’C’棱柱结构特征 有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面围成的多面体。侧棱侧面底面顶点注意:注意:有两个面互相平行,其余各面都是平行四边形的几何体一定是棱柱吗?答:不一定是.如图所示,不是棱柱.棱柱的性质 1. 侧棱都相等,侧面都是平行四边形; 2. 两个底面与平行于底面的截面都是全等的多边形; 3. 平行于侧棱的截面都是平行四边形;1 、按侧棱是否和底面垂直分类:棱柱斜棱柱直棱柱正棱柱其它直棱柱2 、按底面多边形边数分类:棱柱的分类 三棱柱、四棱柱、五棱柱、 ······棱柱的分类按边数分按侧棱是否与底面垂直分斜棱柱 直棱柱 正棱柱三棱柱 四棱柱 五棱柱 四棱柱平行六面体长方体直平行六面体正四棱柱正方体底面变为平行四边形侧棱与底面垂直底面是矩形底面为正方形侧棱与底面边长相等几种六面体的关系:几种六面体的关系:棱锥 SABCD顶点侧面侧棱底面结构特征 有一个面是多边形,其余各面都是有一个公共顶点的三角形。 按底面多边形的边数,可以分为三棱锥、四棱锥、五棱锥、……ABCDS棱锥的分类 正棱锥:底面是正多边形,并且顶点在底面内的射影是底面中心的棱锥。【知识梳理】 棱锥 1 、定义:有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫棱锥。如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面中心,这样的棱锥叫做正棱锥。2 、性质Ⅰ 、正棱锥的性质(1) 各侧棱相等,各侧面都是全等的等腰三角形。(2) 棱锥的高、斜高和斜高在底面上的射影组成一个直角三角形;棱锥的高、侧棱和侧棱在底面上的射影也组成一个直角三角形。正棱锥性质2棱锥的高、斜高和斜高在底面的射影组成一个直角三角形。棱锥的高、侧棱和侧棱在底面的射影组成一个直角三角形Rt PEO⊿Rt POB⊿Rt PEB⊿Rt BEO⊿棱台由棱锥截得而成,所以在棱台中也有类似的直角梯形。棱台结构特征ABCDA’B’C’D’ 用一个...