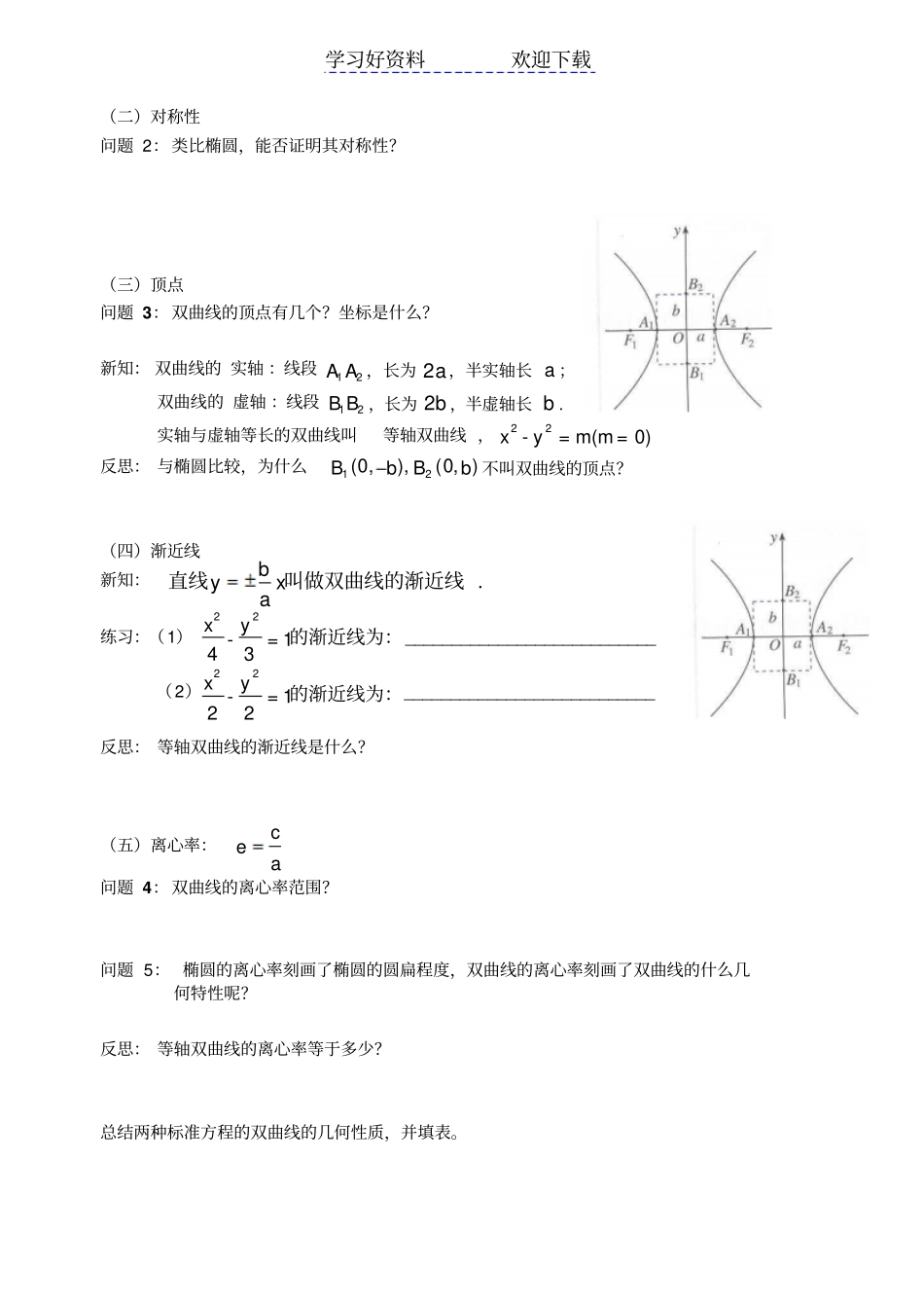
学习好资料欢迎下载2.3.2 双曲线的简单几何性质(学案)一、学习目标:(1)通过对双曲线标准方程的讨论,掌握双曲线的范围、对称性、顶点、渐近线和离心率等几何性质。(2)了解双曲线中心、实轴、虚轴、渐近线等概念,以及它们的关系及其几何意义。二、学习重点、难点:学习重点: 双曲线的简单几何性质。学习难点: 双曲线的离心率和渐近线。三、学习方法: 自主探究合作交流四、学习思路:通过类比椭圆的几何性质,然后利用双曲线的图象探究它的几何性质,再利用几何性质解决实际问题。五、知识链接:复习 1:双曲线的定义和标准方程是什么?复习 2:椭圆有哪些简单几何性质?以焦点在x 轴上的椭圆为例。六、 自主学习:思考: 如果我们也按照椭圆的几何性质的研究方法来研究双曲线,那么双曲线将会具有什么样的几何性质呢?探究一:双曲线简单的几何性质以方程12222byax为例研究双曲线的简单几何性质(一)范围问题 1:类比椭圆,从双曲线方程如何研究其范围?2222+= 1(>> 0)xyabab学习好资料欢迎下载(二)对称性问题 2:类比椭圆,能否证明其对称性?(三)顶点问题 3:双曲线的顶点有几个?坐标是什么?新知: 双曲线的 实轴 :线段12A A ,长为 2a,半实轴长 a ;双曲线的 虚轴 :线段12B B ,长为 2b ,半虚轴长 b . 实轴与虚轴等长的双曲线叫等轴双曲线 ,22- y=xm(m = 0)反思: 与椭圆比较,为什么),0(),,0(21bBbB不叫双曲线的顶点?(四)渐近线新知:练习:(1)___________________________(2)___________________________ 反思: 等轴双曲线的渐近线是什么?(五)离心率:ace问题 4:双曲线的离心率范围?问题 5: 椭圆的离心率刻画了椭圆的圆扁程度,双曲线的离心率刻画了双曲线的什么几何特性呢?反思: 等轴双曲线的离心率等于多少?总结两种标准方程的双曲线的几何性质,并填表。byxa直线叫做双曲线的渐近线 .22-= 143xy的渐近线为:22-= 122xy的渐近线为:学习好资料欢迎下载图形标准方程范围对称性顶点渐近线离心率探究二:性质的应用例 1 已知双曲线的焦点在x 轴上,中心在原点,如果焦距为8,实轴长为6,求此双曲线的标准方程及其离心率。例 2 求双曲线22169144xy的实轴长和虚轴长,顶点坐标,焦点坐标及渐近线方程。六.当堂练习1.求下列双曲线的实轴长,和虚轴长,焦点坐标,离心率及渐近线方程:(1) x2-y2=4 (2)-9x2+y2=81 学习好资料欢迎下载(3)2212516xy(...