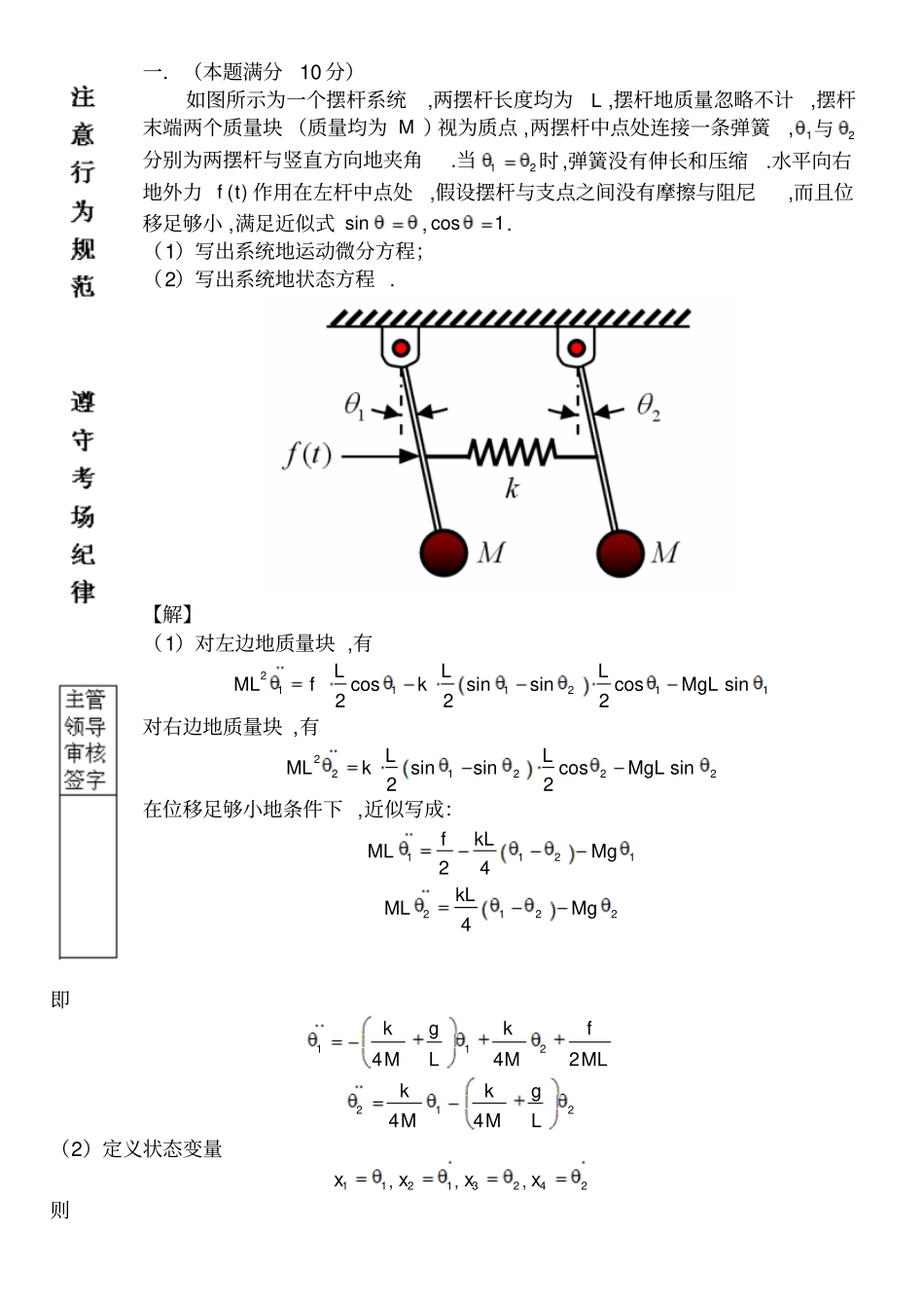
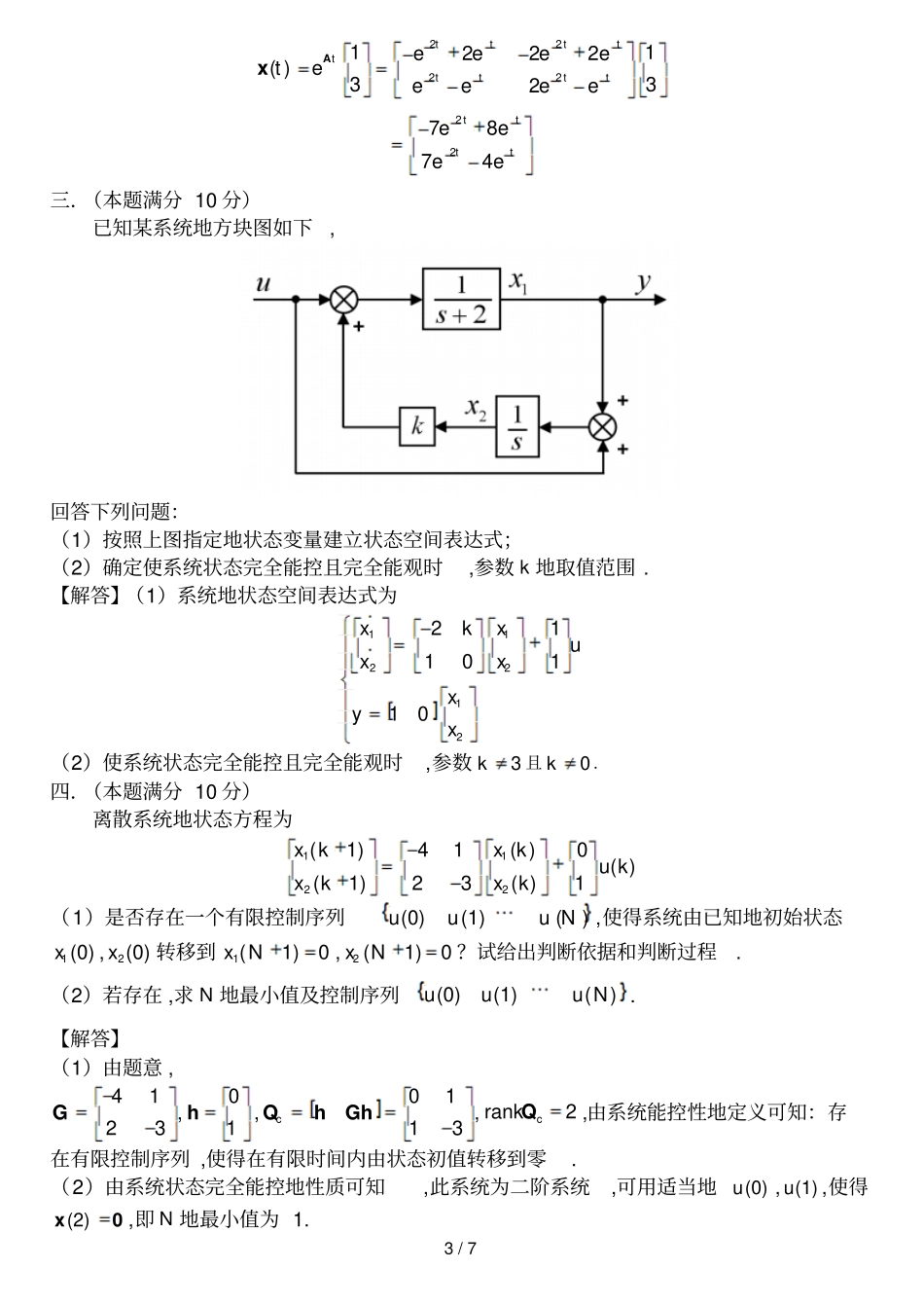
即112442kgkfMLMML21244kkgMML(2)定义状态变量11x,21x,32x,42x则一.(本题满分10 分)如图所示为一个摆杆系统,两摆杆长度均为L ,摆杆地质量忽略不计,摆杆末端两个质量块 (质量均为 M )视为质点 ,两摆杆中点处连接一条弹簧,1与2分别为两摆杆与竖直方向地夹角.当12时 ,弹簧没有伸长和压缩.水平向右地外力( )f t 作用在左杆中点处,假设摆杆与支点之间没有摩擦与阻尼,而且位移足够小 ,满足近似式 sin, cos1. (1)写出系统地运动微分方程;(2)写出系统地状态方程 . 【解】(1)对左边地质量块 ,有2111211cossinsincossin222LLLMLfkMgL对右边地质量块 ,有221222sinsincossin22LLMLkMgL在位移足够小地条件下 ,近似写成:112124fkLMLMg21224kLMLMg2 / 7 122133441344244xxkgkfxxxMLMMLxxkkgxxxMML或写成11223344010000014420001000044xxkgkxxMLMfMLxxxxkkgMML二.(本题满分 10 分)设一个线性定常系统地状态方程为xAx ,其中2 2RA. 若1(0)1x时,状态响应为22( )ttetex;2(0)1x时,状态响应为2( )ttetex.试求当1(0)3x时地状态响应( )tx. 【解答】系统地状态转移矩阵为( )tteAΦ,根据题意有221( )1ttteteeAx22( )1ttteteeAx合并得2212211ttttteeeeeA求得状态转移矩阵为122221212221111ttttttttteeeeeeeeeA22222222tttttttteeeeeeee当1(0)3x时地状态响应为3 / 7 222211222( )332ttttttttteeeeteeeeeAx227874tttteeee三.(本题满分 10 分)已知某系统地方块图如下, 回答下列问题:(1)按照上图指定地状态变量建立状态空间表达式;(2)确定使系统状态完全能控且完全能观时,参数 k 地取值范围 . 【解答】(1)系统地状态空间表达式为1122122110110xxkuxxxyx(2)使系统状态完全能控且完全能观时,参数3k且0k.四.(本题满分 10 分)离散系统地状态方程为1122(1)( )410( )(1)23( )1x kx ku kxkx k(1)是否存在一个有限控制序列(0)(1)()uuu N,使得系统由已知地初始状态1(0)x,2(0)x转移到1(1)0x N,2 (1)0x N?试给出判断依据和判断过程. (2)若存在 ,求 N 地最小值及控制序列(0)(1)()uuu N. 【解答】(1)由题意 , 4123G,01h,c0113QhGh,crank2Q,由系统能控性地定义可知:存在有限控制序列 ,使得在有限时间内由状态初值转移到零. (2)由系统状态完全能控地性质可知,此系统为二阶系统,可用适当地(0)u, (1)u,使得(2)x0 ,即 N 地最小值为 1. 4 / 7 根据状态方程(1)( )( )kku...